दशमलव भिन्न में दशमांश कहाँ हैं? दशमलव भिन्न और उनके साथ संक्रियाएँ

एक सामान्य भिन्न (या मिश्रित संख्या) जिसमें हर एक के बाद एक या अधिक शून्य होते हैं (अर्थात 10, 100, 1000, आदि):

सरल रूप में लिखा जा सकता है: हर के बिना, पूर्णांक और भिन्नात्मक भागों को एक दूसरे से अल्पविराम से अलग करना (इस मामले में, यह माना जाता है कि उचित भिन्न का पूर्णांक भाग 0 के बराबर है)। सबसे पहले पूरा भाग लिखा जाता है, फिर अल्पविराम लगाया जाता है और उसके बाद भिन्नात्मक भाग लिखा जाता है:

इस रूप में लिखी गई सामान्य भिन्न (या मिश्रित संख्याएँ) कहलाती हैं दशमलव.

दशमलव पढ़ना और लिखना

दशमलव भिन्नों को उन्हीं नियमों के अनुसार लिखा जाता है जिनका उपयोग दशमलव संख्या प्रणाली में प्राकृतिक संख्याओं को लिखने के लिए किया जाता है। इसका मतलब यह है कि दशमलव में, प्राकृतिक संख्याओं की तरह, प्रत्येक अंक उन इकाइयों को व्यक्त करता है जो दाईं ओर की पड़ोसी इकाइयों से दस गुना बड़ी होती हैं।

निम्नलिखित प्रविष्टि पर विचार करें:

संख्या 8 अभाज्य इकाइयों को दर्शाती है। संख्या 3 का मतलब ऐसी इकाइयाँ हैं जो साधारण इकाइयों से 10 गुना छोटी हैं, यानी दशमांश। 4 का अर्थ है सौवां, 2 का अर्थ है हजारवां, आदि।

दशमलव बिंदु के बाद दाईं ओर दिखाई देने वाली संख्याओं को कहा जाता है दशमलव.

दशमलव भिन्नों को इस प्रकार पढ़ा जाता है: पहले पूर्ण भाग कहा जाता है, फिर भिन्नात्मक भाग कहा जाता है। किसी पूरे भाग को पढ़ते समय हमेशा इस प्रश्न का उत्तर देना चाहिए: पूरे भाग में कितनी पूर्ण इकाइयाँ हैं? . संपूर्ण इकाइयों की संख्या के आधार पर, उत्तर में संपूर्ण शब्द (या पूर्णांक) जोड़ा जाता है। उदाहरण के लिए, एक पूर्णांक, दो पूर्णांक, तीन पूर्णांक, आदि। भिन्नात्मक भाग को पढ़ते समय, अंशों की संख्या बताई जाती है और अंत में वे उन अंशों का नाम जोड़ते हैं जिनके साथ भिन्नात्मक भाग समाप्त होता है:

3.1 इस प्रकार है: तीन बिंदु एक।

2.017 इस प्रकार पढ़ता है: दो दशमलव सत्रह हज़ारवाँ भाग।

दशमलव भिन्नों को लिखने और पढ़ने के नियमों को बेहतर ढंग से समझने के लिए अंकों की तालिका और उसमें दी गई संख्याओं को लिखने के उदाहरणों पर विचार करें:

कृपया ध्यान दें कि दशमलव बिंदु के बाद उतने ही अंक होते हैं जितने संगत साधारण भिन्न के हर में शून्य होते हैं:

इस ट्यूटोरियल में हम इनमें से प्रत्येक ऑपरेशन को अलग से देखेंगे।

पाठ सामग्री

दशमलव जोड़ना

जैसा कि हम जानते हैं, दशमलव भिन्न में एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव जोड़ते समय पूर्णांक और भिन्नात्मक भाग अलग-अलग जोड़े जाते हैं।

उदाहरण के लिए, आइए दशमलव भिन्न 3.2 और 5.3 जोड़ें। किसी कॉलम में दशमलव भिन्नों को जोड़ना अधिक सुविधाजनक है।

आइए पहले इन दो भिन्नों को एक कॉलम में लिखें, पूर्णांक भाग पूर्णांक के नीचे होने चाहिए, और भिन्न भिन्न के नीचे होने चाहिए। स्कूल में इस आवश्यकता को कहा जाता है "अल्पविराम के अंतर्गत अल्पविराम".

आइए भिन्नों को एक कॉलम में लिखें ताकि अल्पविराम अल्पविराम के नीचे रहे:

हम भिन्नात्मक भागों को जोड़ना शुरू करते हैं: 2 + 3 = 5। हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम पूरे भाग को जोड़ते हैं: 3 + 5 = 8. हम अपने उत्तर के पूरे भाग में आठ लिखते हैं:

अब हम पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं। ऐसा करने के लिए हम फिर से नियम का पालन करते हैं "अल्पविराम के अंतर्गत अल्पविराम":

हमें 8.5 का उत्तर मिला. अतः व्यंजक 3.2 + 5.3, 8.5 के बराबर है

वास्तव में, सब कुछ उतना सरल नहीं है जितना पहली नज़र में लगता है। यहां नुकसान भी हैं, जिनके बारे में हम अभी बात करेंगे।

दशमलव में स्थान

सामान्य संख्याओं की तरह दशमलव भिन्नों के भी अपने अंक होते हैं। ये दसवें के स्थान, सौवें के स्थान, हजारवें के स्थान हैं। इस मामले में, अंक दशमलव बिंदु के बाद शुरू होते हैं।

दशमलव बिंदु के बाद का पहला अंक दसवें स्थान के लिए जिम्मेदार है, दशमलव बिंदु के बाद दूसरा अंक सौवें स्थान के लिए, और दशमलव बिंदु के बाद तीसरा अंक हजारवें स्थान के लिए जिम्मेदार है।

दशमलव स्थानों में कुछ उपयोगी जानकारी होती है। विशेष रूप से, वे आपको बताते हैं कि एक दशमलव में कितने दसवें, सौवें और हज़ारवें भाग होते हैं।

उदाहरण के लिए, दशमलव अंश 0.345 पर विचार करें

वह स्थिति जहां तीनों स्थित हैं, कहलाती है दसवां स्थान

वह स्थिति जहां चारों स्थित हैं, कहलाती है सौवां स्थान

वह स्थिति जहां पांच स्थित हैं, कहलाती है हज़ारवाँ स्थान

आइए इस चित्र को देखें. हम देखते हैं कि दसवें स्थान पर तीन है। इसका मतलब यह है कि दशमलव भिन्न 0.345 में तीन दसवें भाग होते हैं।

यदि हम भिन्नों को जोड़ते हैं, तो हमें मूल दशमलव भिन्न 0.345 प्राप्त होता है

यह देखा जा सकता है कि पहले तो हमें उत्तर मिला, लेकिन हमने इसे दशमलव अंश में बदल दिया और 0.345 प्राप्त हुआ।

दशमलव भिन्नों को जोड़ते समय उन्हीं सिद्धांतों और नियमों का पालन किया जाता है जैसे सामान्य संख्याओं को जोड़ते समय किया जाता है। दशमलव भिन्नों का योग अंकों में होता है: दसवें को दसवें में जोड़ा जाता है, सौवें को सौवें में, हजारवें को हजारवें में जोड़ा जाता है।

इसलिए, दशमलव भिन्नों को जोड़ते समय, आपको नियम का पालन करना चाहिए "अल्पविराम के अंतर्गत अल्पविराम". अल्पविराम के अंतर्गत अल्पविराम वही क्रम प्रदान करता है जिसमें दसवें को दसवें, सौवें को सौवें, हजारवें को हजारवें में जोड़ा जाता है।

उदाहरण 1।व्यंजक 1.5 + 3.4 का मान ज्ञात कीजिए

सबसे पहले, हम भिन्नात्मक भाग 5 + 4 = 9 जोड़ते हैं। हम अपने उत्तर के भिन्नात्मक भाग में नौ लिखते हैं:

अब हम पूर्णांक भाग 1 + 3 = 4 जोड़ते हैं। हम अपने उत्तर के पूर्णांक भाग में चार लिखते हैं:

अब हम पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं। ऐसा करने के लिए, हम फिर से "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हैं:

हमें 4.9 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 1.5 + 3.4 का मान 4.9 है

उदाहरण 2.व्यंजक का मान ज्ञात कीजिए: 3.51 + 1.22

हम इस अभिव्यक्ति को "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं।

सबसे पहले, हम भिन्नात्मक भाग को जोड़ते हैं, अर्थात् 1+2=3 का सौवां भाग। हम अपने उत्तर के सौवें भाग में त्रिक लिखते हैं:

अब दशमांश 5+2=7 जोड़ें। हम अपने उत्तर के दसवें भाग में सात लिखते हैं:

अब हम पूरे भागों को जोड़ते हैं 3+1=4. हम अपने उत्तर के पूरे भाग में चार लिखते हैं:

हम "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए, पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करते हैं:

हमें जो उत्तर मिला वह 4.73 था। इसका मतलब है कि अभिव्यक्ति 3.51 + 1.22 का मान 4.73 के बराबर है

3,51 + 1,22 = 4,73

नियमित संख्याओं की तरह, दशमलव जोड़ते समय, . इस मामले में, उत्तर में एक अंक लिखा जाता है, और बाकी को अगले अंक में स्थानांतरित कर दिया जाता है।

उदाहरण 3.व्यंजक 2.65 + 3.27 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को कॉलम में लिखते हैं:

सौवें भाग को जोड़ें 5+7=12. संख्या 12 हमारे उत्तर के सौवें भाग में फिट नहीं बैठेगी। इसलिए, सौवें भाग में हम संख्या 2 लिखते हैं, और इकाई को अगले अंक पर ले जाते हैं:

अब हम 6 + 2 = 8 का दसवाँ भाग और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 9 मिलता है। हम अपने उत्तर के दसवें में संख्या 9 लिखते हैं:

अब हम पूरे भागों को जोड़ते हैं 2+3=5. हम अपने उत्तर के पूर्णांक भाग में संख्या 5 लिखते हैं:

हमें जो उत्तर मिला वह 5.92 था। इसका मतलब है कि अभिव्यक्ति 2.65 + 3.27 का मान 5.92 के बराबर है

2,65 + 3,27 = 5,92

उदाहरण 4.व्यंजक 9.5 + 2.8 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को कॉलम में लिखते हैं

हम भिन्नात्मक भाग 5 + 8 = 13 जोड़ते हैं। संख्या 13 हमारे उत्तर के भिन्नात्मक भाग में फिट नहीं होगी, इसलिए हम पहले संख्या 3 लिखते हैं, और इकाई को अगले अंक में ले जाते हैं, या यों कहें कि इसे स्थानांतरित करते हैं। पूर्णांक भाग:

अब हम पूर्णांक भाग 9+2=11 और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 12 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 12 लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें उत्तर 12.3 प्राप्त हुआ। इसका मतलब है कि अभिव्यक्ति 9.5 + 2.8 का मान 12.3 है

9,5 + 2,8 = 12,3

दशमलव जोड़ते समय, दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान होनी चाहिए। यदि पर्याप्त संख्याएँ नहीं हैं, तो भिन्नात्मक भाग में ये स्थान शून्य से भरे हुए हैं।

उदाहरण 5. व्यंजक का मान ज्ञात कीजिए: 12.725 + 1.7

इस अभिव्यक्ति को एक कॉलम में लिखने से पहले, आइए दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान कर लें। दशमलव भिन्न 12.725 में दशमलव बिंदु के बाद तीन अंक होते हैं, लेकिन भिन्न 1.7 में केवल एक अंक होता है। इसका मतलब है कि भिन्न 1.7 में आपको अंत में दो शून्य जोड़ने होंगे। तब हमें भिन्न 1.700 प्राप्त होता है। अब आप इस अभिव्यक्ति को एक कॉलम में लिख सकते हैं और गणना शुरू कर सकते हैं:

हजारवें भाग को जोड़ें 5+0=5. हम अपने उत्तर के हज़ारवें भाग में संख्या 5 लिखते हैं:

सैकड़ावाँ भाग 2+0=2 जोड़ें। हम अपने उत्तर के सौवें भाग में संख्या 2 लिखते हैं:

दहाई जोड़ें 7+7=14. संख्या 14 हमारे उत्तर के दसवें हिस्से में फिट नहीं बैठेगी। इसलिए, हम पहले संख्या 4 लिखते हैं, और इकाई को अगले अंक पर ले जाते हैं:

अब हम पूर्णांक भाग 12+1=13 और पिछले ऑपरेशन से प्राप्त इकाई को जोड़ते हैं, हमें 14 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 14 लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 14,425 की प्रतिक्रिया मिली। इसका मतलब है कि अभिव्यक्ति 12.725+1.700 का मान 14.425 है

12,725+ 1,700 = 14,425

दशमलव घटाना

दशमलव अंशों को घटाते समय, आपको उन्हीं नियमों का पालन करना चाहिए जो जोड़ते समय करते हैं: "दशमलव बिंदु के नीचे अल्पविराम" और "दशमलव बिंदु के बाद अंकों की समान संख्या।"

उदाहरण 1।व्यंजक 2.5 − 2.2 का मान ज्ञात कीजिए

हम इस अभिव्यक्ति को "अल्पविराम के अंतर्गत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं:

हम भिन्नात्मक भाग 5−2=3 की गणना करते हैं। हम अपने उत्तर के दसवें भाग में संख्या 3 लिखते हैं:

हम पूर्णांक भाग 2−2=0 की गणना करते हैं। हम अपने उत्तर के पूर्णांक भाग में शून्य लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 0.3 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 2.5 − 2.2 का मान 0.3 के बराबर है

2,5 − 2,2 = 0,3

उदाहरण 2.व्यंजक 7.353 - 3.1 का मान ज्ञात कीजिए

इस अभिव्यक्ति में दशमलव स्थानों की भिन्न संख्या है। भिन्न 7.353 में दशमलव बिंदु के बाद तीन अंक होते हैं, लेकिन भिन्न 3.1 में केवल एक अंक होता है। इसका मतलब यह है कि भिन्न 3.1 में आपको दोनों भिन्नों में अंकों की संख्या समान बनाने के लिए अंत में दो शून्य जोड़ने होंगे। तो हमें 3,100 मिलते हैं.

अब आप इस अभिव्यक्ति को एक कॉलम में लिख सकते हैं और इसकी गणना कर सकते हैं:

हमें 4,253 की प्रतिक्रिया मिली। इसका मतलब है कि अभिव्यक्ति 7.353 - 3.1 का मान 4.253 के बराबर है

7,353 — 3,1 = 4,253

सामान्य संख्याओं की तरह, यदि घटाव असंभव हो जाए तो कभी-कभी आपको आसन्न अंक से एक अंक उधार लेना होगा।

उदाहरण 3.व्यंजक 3.46 − 2.39 का मान ज्ञात कीजिए

6−9 का सैकड़ावाँ भाग घटाएँ। आप संख्या 6 में से संख्या 9 नहीं घटा सकते। इसलिए, आपको आसन्न अंक में से एक अंक उधार लेना होगा। आसन्न अंक में से एक को उधार लेने पर, संख्या 6 संख्या 16 में बदल जाती है। अब आप 16−9=7 के सौवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के सौवें भाग में सात लिखते हैं:

अब हम दसवाँ भाग घटाते हैं। चूँकि हमने दसवें स्थान पर एक इकाई ले ली, इसलिए वहाँ स्थित आंकड़ा एक इकाई कम हो गया। दूसरे शब्दों में, दसवें स्थान पर अब संख्या 4 नहीं, बल्कि संख्या 3 है। आइए 3−3=0 के दसवें हिस्से की गणना करें। हम अपने उत्तर के दसवें भाग में शून्य लिखते हैं:

अब हम पूर्ण भाग 3−2=1 घटाते हैं। हम अपने उत्तर के पूर्णांक भाग में एक लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें 1.07 का उत्तर मिला. इसका मतलब है कि व्यंजक 3.46−2.39 का मान 1.07 के बराबर है

3,46−2,39=1,07

उदाहरण 4. व्यंजक 3−1.2 का मान ज्ञात कीजिए

यह उदाहरण एक पूर्ण संख्या से दशमलव घटाता है। आइए इस अभिव्यक्ति को एक कॉलम में लिखें ताकि दशमलव अंश 1.23 का पूरा भाग संख्या 3 के अंतर्गत हो

अब दशमलव बिंदु के बाद अंकों की संख्या समान कर लेते हैं। ऐसा करने के लिए, संख्या 3 के बाद हम अल्पविराम लगाते हैं और एक शून्य जोड़ते हैं:

अब हम दसवां हिस्सा घटाते हैं: 0−2. आप संख्या 2 को शून्य से नहीं घटा सकते, इसलिए, आपको आसन्न अंक में से एक अंक लेने की आवश्यकता है। पड़ोसी अंक से एक उधार लेने पर, 0 संख्या 10 में बदल जाता है। अब आप 10−2=8 के दसवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के दसवें भाग में आठ लिखते हैं:

अब हम पूरे भागों को घटाते हैं। पहले, संख्या 3 संपूर्ण में स्थित थी, लेकिन हमने इसमें से एक इकाई ले ली। परिणामस्वरूप, यह संख्या 2 में बदल गया। इसलिए, 2 से हम 1 घटाते हैं। 2−1=1। हम अपने उत्तर के पूर्णांक भाग में एक लिखते हैं:

पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करें:

हमें जो उत्तर मिला वह 1.8 था। इसका मतलब है कि व्यंजक 3−1.2 का मान 1.8 है

दशमलव को गुणा करना

दशमलव को गुणा करना सरल भी है और मज़ेदार भी। दशमलव को गुणा करने के लिए, आप अल्पविरामों को अनदेखा करते हुए, उन्हें नियमित संख्याओं की तरह गुणा करें।

उत्तर प्राप्त करने के बाद, आपको पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी, फिर उत्तर में दाईं ओर से समान अंकों की संख्या गिननी होगी और अल्पविराम लगाना होगा।

उदाहरण 1।व्यंजक 2.5 × 1.5 का मान ज्ञात कीजिए

आइए अल्पविरामों को अनदेखा करते हुए, इन दशमलव भिन्नों को सामान्य संख्याओं की तरह गुणा करें। अल्पविरामों को अनदेखा करने के लिए, आप अस्थायी रूप से कल्पना कर सकते हैं कि वे पूरी तरह से अनुपस्थित हैं:

हमें 375 मिला। इस संख्या में, आपको पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.5 और 1.5 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। पहले भिन्न में दशमलव बिंदु के बाद एक अंक होता है, दूसरे भिन्न में भी एक अंक होता है। कुल दो नंबर.

हम संख्या 375 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 3.75 का उत्तर मिला. अतः व्यंजक 2.5 × 1.5 का मान 3.75 है

2.5 × 1.5 = 3.75

उदाहरण 2.व्यंजक 12.85 × 2.7 का मान ज्ञात कीजिए

आइए अल्पविरामों को अनदेखा करते हुए, इन दशमलव भिन्नों को गुणा करें:

हमें 34695 प्राप्त हुआ। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 12.85 और 2.7 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 12.85 में दशमलव बिंदु के बाद दो अंक होते हैं, और भिन्न 2.7 में एक अंक होता है - कुल तीन अंक।

हम संख्या 34695 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 34,695 का रिस्पॉन्स मिला. अतः व्यंजक 12.85 × 2.7 का मान 34.695 है

12.85 × 2.7 = 34.695

दशमलव को एक नियमित संख्या से गुणा करना

कभी-कभी ऐसी स्थितियाँ उत्पन्न होती हैं जब आपको दशमलव भिन्न को किसी नियमित संख्या से गुणा करने की आवश्यकता होती है।

दशमलव और संख्या को गुणा करने के लिए, आप दशमलव में अल्पविराम पर ध्यान दिए बिना उन्हें गुणा करते हैं। उत्तर प्राप्त करने के बाद, आपको पूर्ण भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव भिन्न में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी, फिर उत्तर में दाईं ओर से अंकों की समान संख्या गिननी होगी और अल्पविराम लगाना होगा।

उदाहरण के लिए, 2.54 को 2 से गुणा करें

अल्पविराम को अनदेखा करते हुए, दशमलव भिन्न 2.54 को सामान्य संख्या 2 से गुणा करें:

हमें संख्या 508 मिली। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.54 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 2.54 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 508 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 5.08 का जवाब मिला. अतः व्यंजक 2.54 × 2 का मान 5.08 है

2.54 × 2 = 5.08

दशमलव को 10, 100, 1000 से गुणा करना

दशमलव को 10, 100, या 1000 से गुणा करना उसी तरह से किया जाता है जैसे दशमलव को नियमित संख्याओं से गुणा करना। आपको दशमलव अंश में अल्पविराम पर ध्यान न देते हुए गुणन करना है, फिर उत्तर में, पूरे भाग को भिन्नात्मक भाग से अलग करना है, दाईं ओर से अंकों की उतनी ही संख्या गिननी है जितनी दशमलव बिंदु के बाद अंक थे।

उदाहरण के लिए, 2.88 को 10 से गुणा करें

दशमलव भिन्न में अल्पविराम को अनदेखा करते हुए, दशमलव भिन्न 2.88 को 10 से गुणा करें:

हमें 2880 मिला। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 2.88 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। हम देखते हैं कि भिन्न 2.88 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 2880 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

हमें 28.80 का जवाब मिला. आइए अंतिम शून्य को हटा दें और 28.8 प्राप्त करें। इसका मतलब है कि अभिव्यक्ति 2.88×10 का मान 28.8 है

2.88 × 10 = 28.8

दशमलव भिन्नों को 10, 100, 1000 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। इसमें दशमलव बिंदु को दाईं ओर उतने अंकों तक ले जाना शामिल है जितने गुणनखंड में शून्य हैं।

उदाहरण के लिए, आइए पिछले उदाहरण 2.88×10 को इस प्रकार हल करें। कोई गणना दिए बिना, हम तुरंत कारक 10 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें एक शून्य है। अब भिन्न 2.88 में हम दशमलव बिंदु को दाएँ एक अंक तक ले जाते हैं, हमें 28.8 प्राप्त होता है।

2.88 × 10 = 28.8

आइए 2.88 को 100 से गुणा करने का प्रयास करें। हम तुरंत कारक 100 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें दो शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को दाएँ दो अंकों तक ले जाते हैं, हमें 288 मिलता है

2.88 × 100 = 288

आइए 2.88 को 1000 से गुणा करने का प्रयास करें। हम तुरंत कारक 1000 को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाते हैं। वहां कोई तीसरा अंक नहीं है, इसलिए हम एक और शून्य जोड़ते हैं। परिणामस्वरूप, हमें 2880 मिलते हैं।

2.88 × 1000 = 2880

दशमलव को 0.1 0.01 और 0.001 से गुणा करना

दशमलव को 0.1, 0.01, और 0.001 से गुणा करना उसी तरह काम करता है जैसे दशमलव को दशमलव से गुणा करना। भिन्नों को सामान्य संख्याओं की तरह गुणा करना और उत्तर में अल्पविराम लगाना, दाहिनी ओर उतने ही अंक गिनना आवश्यक है जितने दोनों भिन्नों में दशमलव बिंदु के बाद अंक हों।

उदाहरण के लिए, 3.25 को 0.1 से गुणा करें

हम इन भिन्नों को सामान्य संख्याओं की तरह गुणा करते हैं, अल्पविरामों को अनदेखा करते हुए:

हमें 325 मिला। इस संख्या में आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको भिन्न 3.25 और 0.1 में दशमलव बिंदु के बाद अंकों की संख्या गिननी होगी। भिन्न 3.25 में दशमलव बिंदु के बाद दो अंक होते हैं, और भिन्न 0.1 में एक अंक होता है। कुल तीन नंबर.

हम संख्या 325 पर लौटते हैं और दाएं से बाएं ओर जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने होंगे और अल्पविराम लगाना होगा। तीन अंक गिनने के बाद पता चलता है कि अंक खत्म हो गए हैं। इस मामले में, आपको एक शून्य जोड़ना होगा और अल्पविराम जोड़ना होगा:

हमें 0.325 का उत्तर मिला। इसका मतलब है कि अभिव्यक्ति 3.25 × 0.1 का मान 0.325 है

3.25 × 0.1 = 0.325

दशमलव को 0.1, 0.01 और 0.001 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। इसमें दशमलव बिंदु को बाईं ओर उतने अंकों तक ले जाना शामिल है जितने गुणनखंड में शून्य हैं।

उदाहरण के लिए, आइए पिछले उदाहरण 3.25 × 0.1 को इस प्रकार हल करें। बिना कोई गणना दिए हम तुरंत 0.1 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें एक शून्य है। अब भिन्न 3.25 में हम दशमलव बिंदु को एक अंक से बाईं ओर ले जाते हैं। अल्पविराम को एक अंक बाईं ओर ले जाने पर, हम देखते हैं कि तीन से पहले कोई और अंक नहीं हैं। इस स्थिति में, एक शून्य जोड़ें और अल्पविराम लगाएं। परिणाम 0.325 है

3.25 × 0.1 = 0.325

आइए 3.25 को 0.01 से गुणा करने का प्रयास करें। हम तुरंत 0.01 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें दो शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को बाएँ दो अंकों पर ले जाते हैं, हमें 0.0325 मिलता है

3.25 × 0.01 = 0.0325

आइए 3.25 को 0.001 से गुणा करने का प्रयास करें। हम तुरंत 0.001 के गुणक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को तीन अंकों से बाईं ओर ले जाते हैं, हमें 0.00325 मिलता है

3.25 × 0.001 = 0.00325

दशमलव भिन्नों को 0.1, 0.001 और 0.001 से गुणा करने को 10, 100, 1000 से गुणा करने में भ्रमित न हों। अधिकांश लोगों के लिए यह एक सामान्य गलती है।

10, 100, 1000 से गुणा करने पर, दशमलव बिंदु दाईं ओर उतने ही अंकों से चला जाता है जितने गुणक में शून्य होते हैं।

और जब 0.1, 0.01 और 0.001 से गुणा किया जाता है, तो दशमलव बिंदु बाईं ओर उतने ही अंकों से चला जाता है, क्योंकि गुणक में शून्य होते हैं।

यदि शुरुआत में याद रखना मुश्किल हो, तो आप पहली विधि का उपयोग कर सकते हैं, जिसमें सामान्य संख्याओं की तरह गुणा किया जाता है। उत्तर में आपको दाहिनी ओर के अंकों की समान संख्या गिनकर पूर्ण भाग को भिन्न भाग से अलग करना होगा क्योंकि दोनों भिन्नों में दशमलव बिंदु के बाद अंक होते हैं।

छोटी संख्या को बड़ी संख्या से भाग देना। अग्रवर्ती स्तर।

पिछले पाठों में से एक में, हमने कहा था कि छोटी संख्या को बड़ी संख्या से विभाजित करने पर, एक भिन्न प्राप्त होता है, जिसका अंश भाज्य होता है, और हर भाजक होता है।

उदाहरण के लिए, एक सेब को दो के बीच विभाजित करने के लिए, आपको अंश में 1 (एक सेब) लिखना होगा, और हर में 2 (दो दोस्त) लिखना होगा। परिणामस्वरूप, हमें भिन्न प्राप्त होता है। इसका मतलब है कि प्रत्येक मित्र को एक सेब मिलेगा। दूसरे शब्दों में, आधा सेब. भिन्न समस्या का उत्तर है "एक सेब को दो भागों में कैसे बाँटें"

यह पता चलता है कि यदि आप 1 को 2 से विभाजित करते हैं तो आप इस समस्या को और अधिक हल कर सकते हैं। आखिरकार, किसी भी भिन्न में भिन्नात्मक रेखा का अर्थ विभाजन होता है, और इसलिए भिन्न में इस विभाजन की अनुमति है। आख़िर कैसे? हम इस तथ्य के आदी हैं कि लाभांश हमेशा भाजक से अधिक होता है। लेकिन यहां, इसके विपरीत, लाभांश भाजक से कम है।

यदि हम यह याद रखें कि अंश का अर्थ कुचलना, विभाजन करना, विभाजन करना है तो सब कुछ स्पष्ट हो जाएगा। इसका मतलब यह है कि इकाई को केवल दो भागों में नहीं, बल्कि जितने चाहें उतने भागों में विभाजित किया जा सकता है।

जब आप किसी छोटी संख्या को बड़ी संख्या से विभाजित करते हैं, तो आपको एक दशमलव अंश मिलता है जिसमें पूर्णांक भाग 0 (शून्य) होता है। भिन्नात्मक भाग कुछ भी हो सकता है।

तो, आइए 1 को 2 से विभाजित करें। आइए इस उदाहरण को एक कोने से हल करें:

एक को पूर्णतः दो भागों में विभाजित नहीं किया जा सकता। यदि आप कोई प्रश्न पूछते हैं "एक में कितने दो होते हैं" , तो उत्तर 0 होगा। इसलिए, भागफल में हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब, हमेशा की तरह, शेषफल प्राप्त करने के लिए हम भागफल को भाजक से गुणा करते हैं:

वह क्षण आ गया है जब इकाई को दो भागों में विभाजित किया जा सकता है। ऐसा करने के लिए, परिणामी शून्य के दाईं ओर एक और शून्य जोड़ें:

हमें 10 प्राप्त हुआ। 10 को 2 से विभाजित करने पर, हमें 5 प्राप्त होता है। हम पाँच को अपने उत्तर के भिन्नात्मक भाग में लिखते हैं:

अब हम गणना पूरी करने के लिए अंतिम शेषफल निकालते हैं। 10 प्राप्त करने के लिए 5 को 2 से गुणा करें

हमें 0.5 का उत्तर मिला. अतः भिन्न 0.5 है

दशमलव अंश 0.5 का उपयोग करके आधा सेब भी लिखा जा सकता है। यदि हम इन दो हिस्सों (0.5 और 0.5) को जोड़ दें, तो हमें फिर से असली पूरा सेब मिलता है:

यह बात तब भी समझ में आ सकती है जब आप कल्पना करें कि 1 सेमी को दो भागों में कैसे विभाजित किया जाता है। यदि आप 1 सेंटीमीटर को 2 भागों में विभाजित करते हैं, तो आपको 0.5 सेमी मिलता है

उदाहरण 2.व्यंजक 4:5 का मान ज्ञात कीजिए

एक चार में कितनी पाँच होती हैं? बिल्कुल नहीं। हम भागफल में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम चार के नीचे एक शून्य लिखते हैं। इस शून्य को लाभांश से तुरंत घटा दें:

अब चारों को 5 भागों में बाँटना शुरू करते हैं। ऐसा करने के लिए, 4 के दाईं ओर एक शून्य जोड़ें और 40 को 5 से विभाजित करें, हमें 8 मिलता है। हम भागफल में आठ लिखते हैं।

हम 40 प्राप्त करने के लिए 8 को 5 से गुणा करके उदाहरण पूरा करते हैं:

हमें 0.8 का उत्तर मिला. इसका मतलब है कि व्यंजक 4:5 का मान 0.8 है

उदाहरण 3.व्यंजक 5:125 का मान ज्ञात कीजिए

पाँच में 125 कितनी संख्याएँ हैं? बिल्कुल नहीं। हम भागफल में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम पाँच के नीचे 0 लिखते हैं। पांच में से तुरंत 0 घटाएं

अब पाँचों को 125 भागों में बाँटना शुरू करते हैं। ऐसा करने के लिए, हम इन पाँच के दाईं ओर एक शून्य लिखते हैं:

50 को 125 से भाग दें। संख्या 50 में 125 कितनी संख्याएँ हैं? बिल्कुल नहीं। अतः भागफल में हम पुनः 0 लिखते हैं

0 को 125 से गुणा करें, हमें 0 मिलता है। इस शून्य को 50 के नीचे लिखें। तुरंत 50 में से 0 घटा दें

अब संख्या 50 को 125 भागों में विभाजित करें। ऐसा करने के लिए, हम 50 के दाईं ओर एक और शून्य लिखते हैं:

500 को 125 से विभाजित करें। संख्या 500 में 125 कितनी संख्याएँ हैं? संख्या 500 में चार संख्याएँ 125 हैं। चारों को भागफल में लिखें:

हम 500 प्राप्त करने के लिए 4 को 125 से गुणा करके उदाहरण पूरा करते हैं

हमें 0.04 का उत्तर मिला. इसका मतलब है कि अभिव्यक्ति 5:125 का मान 0.04 है

बिना किसी शेषफल के संख्याओं को विभाजित करना

तो, चलिए भागफल में इकाई के बाद अल्पविराम लगाते हैं, जिससे यह संकेत मिलता है कि पूर्णांक भागों का विभाजन समाप्त हो गया है और हम भिन्नात्मक भाग की ओर आगे बढ़ रहे हैं:

आइए शेषफल 4 में शून्य जोड़ें

अब 40 को 5 से विभाजित करें, हमें 8 प्राप्त होता है। हम भागफल में आठ लिखते हैं:

40−40=0. हमें 0 बचा है. इसका मतलब है कि विभाजन पूरी तरह से पूरा हो गया है। 9 को 5 से विभाजित करने पर दशमलव भिन्न 1.8 प्राप्त होता है:

9: 5 = 1,8

उदाहरण 2. 84 को बिना किसी शेषफल के 5 से विभाजित करें

सबसे पहले, शेषफल के साथ हमेशा की तरह 84 को 5 से विभाजित करें:

हमें निजी तौर पर 16 मिल गए और 4 और बचे हैं। आइए अब इस शेषफल को 5 से विभाजित करें। भागफल में अल्पविराम लगाएं, और शेष 4 में 0 जोड़ें

अब हम 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम दशमलव बिंदु के बाद भागफल में आठ लिखते हैं:

और यह जांच कर उदाहरण पूरा करें कि क्या अभी भी कुछ शेष है:

दशमलव को एक नियमित संख्या से विभाजित करना

जैसा कि हम जानते हैं, दशमलव भिन्न में एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव अंश को किसी नियमित संख्या से विभाजित करते समय, आपको सबसे पहले यह करना होगा:

• दशमलव भिन्न के पूरे भाग को इस संख्या से विभाजित करें;
• पूरे भाग को विभाजित करने के बाद, आपको तुरंत भागफल में अल्पविराम लगाना होगा और सामान्य विभाजन की तरह गणना जारी रखनी होगी।

उदाहरण के लिए, 4.8 को 2 से विभाजित करें

आइए इस उदाहरण को एक कोने में लिखें:

अब पूरे भाग को 2 से विभाजित करते हैं। चार को दो से विभाजित करने पर दो बराबर होता है। हम भागफल में दो लिखते हैं और तुरंत अल्पविराम लगाते हैं:

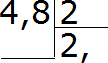
अब हम भागफल को भाजक से गुणा करते हैं और देखते हैं कि भाग से कोई शेषफल बचता है या नहीं:

4−4=0. शेषफल शून्य है. हम अभी तक शून्य नहीं लिखते हैं, क्योंकि समाधान पूरा नहीं हुआ है। इसके बाद, हम सामान्य विभाजन की तरह गणना करना जारी रखेंगे। 8 को हटाएं और इसे 2 से विभाजित करें

8: 2 = 4. हम भागफल में चार लिखते हैं और तुरंत इसे भाजक से गुणा करते हैं:

हमें 2.4 का उत्तर मिला. व्यंजक 4.8:2 का मान 2.4 है

उदाहरण 2.व्यंजक 8.43:3 का मान ज्ञात कीजिए

8 को 3 से विभाजित करने पर हमें 2 प्राप्त होता है। 2 के तुरंत बाद अल्पविराम लगाएं:

अब हम भागफल को भाजक 2 × 3 = 6 से गुणा करते हैं। हम आठ के नीचे छह लिखते हैं और शेषफल ज्ञात करते हैं:

24 को 3 से भाग देने पर 8 प्राप्त होता है। हम भागफल में आठ लिखते हैं। भाग का शेषफल ज्ञात करने के लिए इसे तुरंत भाजक से गुणा करें:

24−24=0. शेषफल शून्य है. हम अभी तक शून्य नहीं लिखते हैं. हम लाभांश से अंतिम तीन हटाते हैं और 3 से विभाजित करते हैं, हमें 1 मिलता है। इस उदाहरण को पूरा करने के लिए तुरंत 1 को 3 से गुणा करें:

हमें जो उत्तर मिला वह 2.81 था। इसका अर्थ है कि व्यंजक 8.43:3 का मान 2.81 है

दशमलव को दशमलव से विभाजित करना

किसी दशमलव भिन्न को दशमलव भिन्न से विभाजित करने के लिए, आपको लाभांश और भाजक में दशमलव बिंदु को दाईं ओर उतने ही अंकों से ले जाना होगा जितना कि भाजक में दशमलव बिंदु के बाद होता है, और फिर सामान्य संख्या से विभाजित करना होगा।

उदाहरण के लिए, 5.95 को 1.7 से विभाजित करें

आइए इस अभिव्यक्ति को एक कोने से लिखें

अब लाभांश और भाजक में हम दशमलव बिंदु को दाईं ओर उतने ही अंकों से ले जाते हैं जितने अंक भाजक में दशमलव बिंदु के बाद होते हैं। भाजक में दशमलव बिंदु के बाद एक अंक होता है। इसका मतलब यह है कि लाभांश और भाजक में हमें दशमलव बिंदु को एक अंक से दाईं ओर ले जाना होगा। हम हस्तांतरण:

दशमलव बिंदु को दाएँ एक अंक तक ले जाने के बाद, दशमलव भिन्न 5.95, भिन्न 59.5 बन गया। और दशमलव भिन्न 1.7, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, सामान्य संख्या 17 में बदल गया। और हम पहले से ही जानते हैं कि दशमलव भिन्न को एक नियमित संख्या से कैसे विभाजित किया जाता है। आगे की गणना कठिन नहीं है:

विभाजन को आसान बनाने के लिए अल्पविराम को दाईं ओर ले जाया जाता है। इसकी अनुमति इसलिए है क्योंकि लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित करने पर भागफल नहीं बदलता है। इसका मतलब क्या है?

यह विभाजन की दिलचस्प विशेषताओं में से एक है। इसे भागफल गुण कहा जाता है। अभिव्यक्ति 9: 3 = 3 पर विचार करें। यदि इस अभिव्यक्ति में लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित किया जाता है, तो भागफल 3 नहीं बदलेगा।

आइए लाभांश और भाजक को 2 से गुणा करें और देखें कि इससे क्या निकलता है:

(9 × 2) : (3 × 2) = 18: 6 = 3

जैसा कि उदाहरण से देखा जा सकता है, भागफल नहीं बदला है।

यही बात तब होती है जब हम लाभांश और भाजक में अल्पविराम लगाते हैं। पिछले उदाहरण में, जहां हमने 5.91 को 1.7 से विभाजित किया था, हमने लाभांश और भाजक में अल्पविराम को एक अंक दाईं ओर ले जाया था। दशमलव बिंदु को स्थानांतरित करने के बाद, अंश 5.91 को अंश 59.1 में बदल दिया गया और अंश 1.7 को सामान्य संख्या 17 में बदल दिया गया।

दरअसल, इस प्रक्रिया के अंदर 10 से गुणा होता था। यह इस तरह दिखता था:

5.91 × 10 = 59.1

इसलिए, भाजक में दशमलव बिंदु के बाद अंकों की संख्या यह निर्धारित करती है कि लाभांश और भाजक को किससे गुणा किया जाएगा। दूसरे शब्दों में, भाजक में दशमलव बिंदु के बाद अंकों की संख्या यह निर्धारित करेगी कि लाभांश में कितने अंक और भाजक में दशमलव बिंदु दाईं ओर ले जाया जाएगा।

दशमलव को 10, 100, 1000 से विभाजित करना

दशमलव को 10, 100, या 1000 से विभाजित करना उसी तरह किया जाता है जैसे। उदाहरण के लिए, 2.1 को 10 से विभाजित करें। एक कोने का उपयोग करके इस उदाहरण को हल करें:

लेकिन एक दूसरा तरीका भी है. यह हल्का है. इस पद्धति का सार यह है कि लाभांश में अल्पविराम को उतने अंकों से बाईं ओर ले जाया जाता है जितने भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस प्रकार हल करें। 2.1:10. हम भाजक को देखते हैं। हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। इसका मतलब है कि 2.1 के लाभांश में आपको दशमलव बिंदु को एक अंक से बाईं ओर ले जाना होगा। हम अल्पविराम को बाएँ एक अंक पर ले जाते हैं और देखते हैं कि कोई और अंक नहीं बचा है। इस स्थिति में, संख्या से पहले एक और शून्य जोड़ें। परिणामस्वरूप हमें 0.21 प्राप्त होता है

आइए 2.1 को 100 से विभाजित करने का प्रयास करें। 100 में दो शून्य हैं। इसका मतलब है कि लाभांश 2.1 में हमें अल्पविराम को दो अंकों से बाईं ओर ले जाना होगा:

2,1: 100 = 0,021

आइए 2.1 को 1000 से विभाजित करने का प्रयास करें। 1000 में तीन शून्य होते हैं। इसका मतलब है कि लाभांश 2.1 में आपको अल्पविराम को तीन अंकों से बाईं ओर ले जाना होगा:

2,1: 1000 = 0,0021

दशमलव को 0.1, 0.01 और 0.001 से विभाजित करना

दशमलव अंश को 0.1, 0.01, और 0.001 से विभाजित करना उसी तरह से किया जाता है। लाभांश और भाजक में, आपको दशमलव बिंदु को दाईं ओर उतने अंकों तक ले जाना होगा जितने अंक भाजक में दशमलव बिंदु के बाद हों।

उदाहरण के लिए, आइए 6.3 को 0.1 से विभाजित करें। सबसे पहले, आइए लाभांश और भाजक में अल्पविरामों को दाईं ओर उतने ही अंकों से ले जाएं जितने अंकों के बाद भाजक में होते हैं। भाजक में दशमलव बिंदु के बाद एक अंक होता है। इसका मतलब है कि हम लाभांश और भाजक में अल्पविराम को एक अंक से दाईं ओर ले जाते हैं।

दशमलव बिंदु को दाएँ एक अंक पर ले जाने के बाद, दशमलव भिन्न 6.3 सामान्य संख्या 63 बन जाता है, और दशमलव भिन्न 0.1 दशमलव बिंदु को दाएँ एक अंक पर ले जाने के बाद एक में बदल जाता है। और 63 को 1 से विभाजित करना बहुत सरल है:

इसका मतलब है कि अभिव्यक्ति 6.3: 0.1 का मान 63 है

लेकिन एक दूसरा तरीका भी है. यह हल्का है. इस पद्धति का सार यह है कि लाभांश में अल्पविराम को उतने अंकों से दाईं ओर ले जाया जाता है जितने भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस प्रकार हल करें। 6.3: 0.1. आइए भाजक को देखें. हमें इसमें रुचि है कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। इसका मतलब है कि 6.3 के लाभांश में आपको दशमलव बिंदु को एक अंक से दाईं ओर ले जाना होगा। अल्पविराम को दाएँ एक अंक पर ले जाएँ और 63 प्राप्त करें

आइए 6.3 को 0.01 से विभाजित करने का प्रयास करें। 0.01 के भाजक में दो शून्य होते हैं। इसका मतलब है कि लाभांश 6.3 में हमें दशमलव बिंदु को दो अंकों से दाईं ओर ले जाना होगा। लेकिन लाभांश में दशमलव बिंदु के बाद केवल एक अंक होता है। इस स्थिति में, आपको अंत में एक और शून्य जोड़ना होगा। परिणामस्वरूप हमें 630 मिलते हैं

आइए 6.3 को 0.001 से विभाजित करने का प्रयास करें। 0.001 के भाजक में तीन शून्य होते हैं। इसका मतलब है कि लाभांश 6.3 में हमें दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाना होगा:

6,3: 0,001 = 6300

स्वतंत्र समाधान के लिए कार्य

क्या आपको पाठ पसंद आया?
हमारे नए VKontakte समूह में शामिल हों और नए पाठों के बारे में सूचनाएं प्राप्त करना शुरू करें

जैसा:

± डी एम … डी 1 डी 0 , डी -1 डी -2 …

जहां ± भिन्न चिह्न है: या तो +, या -,

, एक दशमलव बिंदु है जो किसी संख्या के पूर्णांक और भिन्नात्मक भागों के बीच विभाजक के रूप में कार्य करता है,

डीके- दशमलव संख्याएं।

इस मामले में, दशमलव बिंदु से पहले (इसके बाईं ओर) संख्याओं के क्रम का अंत होता है (प्रति अंक न्यूनतम 1 के रूप में), और दशमलव बिंदु के बाद (दाईं ओर) यह दोनों परिमित हो सकता है (एक विकल्प के रूप में, दशमलव बिंदु के बाद कोई अंक नहीं हो सकता) और अनंत।

दशमलव मान ± डी एम … डी 1 डी 0 , डी -1 डी -2 … एक वास्तविक संख्या है:

जो कि किसी परिमित या अनंत संख्या के पदों के योग के बराबर होता है।

दशमलव भिन्नों का उपयोग करके वास्तविक संख्याओं का प्रतिनिधित्व करना दशमलव संख्या प्रणाली में पूर्णांक लिखने का एक सामान्यीकरण है। पूर्णांक के दशमलव प्रतिनिधित्व में दशमलव बिंदु के बाद कोई अंक नहीं होता है, इसलिए प्रतिनिधित्व इस तरह दिखता है:

± डी एम … डी 1 डी 0 ,

और यह हमारी संख्या को दशमलव संख्या प्रणाली में लिखने से मेल खाता है।

दशमलव- यह 1 को 10, 100, 1000 इत्यादि भागों में विभाजित करने का परिणाम है। ये भिन्न गणना के लिए काफी सुविधाजनक हैं, क्योंकि वे उसी स्थितीय प्रणाली पर आधारित हैं जिस पर पूर्णांकों की गिनती और रिकॉर्डिंग आधारित होती है। इसके लिए धन्यवाद, दशमलव अंशों के साथ काम करने के लिए अंकन और नियम लगभग पूर्ण संख्याओं के समान ही हैं।

दशमलव भिन्न लिखते समय, आपको हर को चिह्नित करने की आवश्यकता नहीं होती है; यह संबंधित अंक द्वारा लिए गए स्थान से निर्धारित होता है। पहले हम संख्या का पूरा भाग लिखते हैं, फिर दाईं ओर दशमलव बिंदु लगाते हैं। दशमलव बिंदु के बाद पहला अंक दसवें की संख्या को इंगित करता है, दूसरा - सौवें की संख्या को, तीसरा - हजारवें की संख्या को, इत्यादि। दशमलव बिंदु के बाद स्थित संख्याएँ हैं दशमलव.

उदाहरण के लिए:

दशमलव भिन्नों का एक लाभ यह है कि उन्हें बहुत आसानी से साधारण भिन्नों में बदला जा सकता है: दशमलव बिंदु के बाद की संख्या (हमारे लिए यह 5047 है) मीटर; भाजकके बराबर होती है एन-10 की घात, कहाँ एन- दशमलव स्थानों की संख्या (हमारे लिए यह है एन=4):

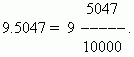
जब दशमलव अंश में कोई पूर्णांक भाग नहीं होता है, तो हम दशमलव बिंदु से पहले एक शून्य लगाते हैं:

दशमलव भिन्नों के गुण.

1. दाईं ओर शून्य जोड़ने पर दशमलव नहीं बदलता है:

13.6 =13.6000.

2. दशमलव के अंत में शून्य हटा देने पर दशमलव नहीं बदलता है:

0.00123000 = 0.00123.

ध्यान!आप वे शून्य नहीं हटा सकते जो दशमलव अंश के अंत में स्थित नहीं हैं!

3. जब हम दशमलव बिंदु को दाईं ओर क्रमशः 1, 2, 2 और इसी तरह के पदों पर ले जाते हैं तो दशमलव भिन्न 10, 100, 1000 और इसी तरह कई बार बढ़ जाती है:

3.675 → 367.5 (अंश सौ गुना बढ़ गया)।

4. जब हम दशमलव बिंदु को बाईं ओर क्रमशः 1, 2, 3, इत्यादि स्थानों पर ले जाते हैं तो दशमलव अंश दस, एक सौ, हजार और इसी तरह कई गुना छोटा हो जाता है:

1536.78 → 1.53678 (अंश एक हजार गुना छोटा हो गया)।

दशमलव भिन्नों के प्रकार.

दशमलव भिन्नों को विभाजित किया गया है अंतिम, अनंतऔर आवधिक दशमलव.

अंतिम दशमलव अंश हैयह एक भिन्न है जिसमें दशमलव बिंदु के बाद अंकों की एक सीमित संख्या होती है (या बिल्कुल भी नहीं होते हैं), यानी। ऐसा लगता है:

एक वास्तविक संख्या को एक परिमित दशमलव भिन्न के रूप में तभी दर्शाया जा सकता है जब यह संख्या तर्कसंगत हो और जब इसे एक अघुलनशील भिन्न के रूप में लिखा जाए पी क्यूभाजक क्यू 2 और 5 के अलावा कोई अभाज्य गुणनखंड नहीं है।

अनंत दशमलव.

इसमें संख्याओं का एक अनंत रूप से दोहराया जाने वाला समूह शामिल है जिसे कहा जाता है अवधि. अवधि कोष्ठक में लिखी गई है। उदाहरण के लिए, 0.12345123451234512345… = 0.(12345).

आवधिक दशमलव- यह एक अनंत दशमलव अंश है जिसमें दशमलव बिंदु के बाद के अंकों का क्रम, एक निश्चित स्थान से शुरू होकर, अंकों का समय-समय पर दोहराया जाने वाला समूह होता है। दूसरे शब्दों में, आवधिक अंश- एक दशमलव अंश जो इस तरह दिखता है:

ऐसा भिन्न आमतौर पर संक्षेप में इस प्रकार लिखा जाता है:

संख्याओं का समूह बी 1 … बी एल, जो दोहराता है, है अंश की अवधि, इस समूह में अंकों की संख्या है अवधि.

जब किसी आवर्त भिन्न में दशमलव बिंदु के तुरंत बाद आवर्त आता है, तो इसका अर्थ है कि भिन्न है शुद्ध आवधिक. जब दशमलव बिंदु और प्रथम आवर्त के बीच संख्याएँ हों, तो भिन्न होती है मिश्रित आवधिक, और दशमलव बिंदु के बाद अवधि के पहले अंक तक अंकों का समूह है अंश पूर्वकाल.

उदाहरण के लिए, भिन्न 1,(23) = 1.2323... शुद्ध आवर्त है, और भिन्न 0.1(23) = 0.12323... मिश्रित आवर्त है।

आवर्त भिन्नों का मुख्य गुण, जिसके कारण वे दशमलव अंशों के पूरे सेट से अलग होते हैं, इस तथ्य में निहित है कि आवधिक अंश और केवल वे तर्कसंगत संख्याओं का प्रतिनिधित्व करते हैं। अधिक सटीक रूप से, निम्नलिखित होता है:

कोई भी अनंत आवधिक दशमलव अंश एक परिमेय संख्या का प्रतिनिधित्व करता है। इसके विपरीत, जब एक परिमेय संख्या को अनंत दशमलव अंश में विस्तारित किया जाता है, तो इसका मतलब है कि यह अंश आवर्त होगा।

इस लेख में हम समझेंगे कि दशमलव भिन्न क्या है, इसमें क्या विशेषताएं और गुण हैं। जाना! 🙂

दशमलव भिन्न साधारण भिन्नों का एक विशेष मामला है (जहाँ हर 10 का गुणज होता है)।

परिभाषा

दशमलव वे भिन्न होते हैं जिनके हर में एक संख्या होती है और उसके बाद कई शून्य होते हैं। अर्थात्, ये 10, 100, 1000, आदि के हर वाले भिन्न हैं। अन्यथा, एक दशमलव अंश को 10 के हर या दस की शक्तियों में से एक के साथ एक अंश के रूप में वर्णित किया जा सकता है।

भिन्नों के उदाहरण:

, ,

दशमलव भिन्नों को सामान्य भिन्नों की तुलना में अलग तरह से लिखा जाता है। इन भिन्नों के साथ संचालन भी सामान्य भिन्नों के साथ संचालन से भिन्न होता है। उनके साथ संचालन के नियम काफी हद तक पूर्णांकों के साथ संचालन के नियमों के समान हैं। यह, विशेष रूप से, व्यावहारिक समस्याओं को हल करने की उनकी मांग को स्पष्ट करता है।

दशमलव संकेतन में भिन्नों का प्रतिनिधित्व

दशमलव अंश में हर नहीं होता है; यह अंश की संख्या प्रदर्शित करता है। सामान्य तौर पर, दशमलव अंश निम्नलिखित योजना के अनुसार लिखा जाता है:

जहाँ X भिन्न का पूर्णांक भाग है, Y उसका भिन्नात्मक भाग है, "," दशमलव बिंदु है।

किसी भिन्न को दशमलव के रूप में सही ढंग से प्रस्तुत करने के लिए, यह आवश्यक है कि यह एक नियमित भिन्न हो, अर्थात, पूर्णांक भाग हाइलाइट किया गया हो (यदि संभव हो) और एक अंश जो हर से कम हो। फिर दशमलव अंकन में पूर्णांक भाग दशमलव बिंदु (X) से पहले लिखा जाता है, और सामान्य अंश का अंश दशमलव बिंदु (Y) के बाद लिखा जाता है।

यदि अंश में हर में शून्य की संख्या से कम अंकों वाली संख्या होती है, तो भाग Y में दशमलव अंकन में अंकों की लुप्त संख्या को अंश अंकों के आगे शून्य से भर दिया जाता है।

उदाहरण:

यदि एक उभयनिष्ठ भिन्न 1 से कम है, अर्थात पूर्णांक भाग नहीं है तो X के लिए दशमलव रूप में 0 लिखें।

भिन्नात्मक भाग (Y) में, अंतिम महत्वपूर्ण (गैर-शून्य) अंक के बाद, शून्य की एक मनमानी संख्या दर्ज की जा सकती है। इससे भिन्न के मान पर कोई प्रभाव नहीं पड़ता. इसके विपरीत, दशमलव के भिन्नात्मक भाग के अंत में सभी शून्य को छोड़ा जा सकता है।

दशमलव पढ़ना

भाग X को आम तौर पर इस प्रकार पढ़ा जाता है: "X पूर्णांक।"

Y भाग को हर में मौजूद संख्या के अनुसार पढ़ा जाता है। हर 10 के लिए आपको पढ़ना चाहिए: "वाई दसवां", हर 100 के लिए: "वाई सौवां", हर 1000 के लिए: "वाई हजारवां" और इसी तरह... 😉

भिन्नात्मक भाग के अंकों की संख्या की गणना के आधार पर पढ़ने का एक अन्य तरीका अधिक सही माना जाता है। ऐसा करने के लिए, आपको यह समझने की आवश्यकता है कि भिन्नात्मक अंक भिन्न के पूरे भाग के अंकों के संबंध में दर्पण छवि में स्थित होते हैं।

सही पढ़ने के नाम तालिका में दिए गए हैं:

इसके आधार पर भिन्नात्मक भाग के अंतिम अंक के अंक के नाम के अनुपालन के आधार पर पठन किया जाना चाहिए।

• 3.5 में लिखा है "तीन दशमलव पांच"
• 0.016 में लिखा है "शून्य दशमलव सोलह हजारवां"

एक मनमाना भिन्न को दशमलव में बदलना

यदि किसी सामान्य भिन्न का हर 10 या कुछ घात दस है, तो भिन्न का रूपांतरण ऊपर बताए अनुसार किया जाता है। अन्य स्थितियों में, अतिरिक्त परिवर्तनों की आवश्यकता होती है।

अनुवाद की 2 विधियाँ हैं.

प्रथम स्थानांतरण विधि

अंश और हर को ऐसे पूर्णांक से गुणा किया जाना चाहिए कि हर संख्या 10 या दस की घातों में से एक उत्पन्न करे। और फिर अंश को दशमलव संकेतन में दर्शाया जाता है।

यह विधि उन भिन्नों के लिए लागू होती है जिनके हर को केवल 2 और 5 में ही विस्तारित किया जा सकता है। इसलिए, पिछले उदाहरण में . यदि विस्तार में अन्य प्रमुख कारक शामिल हैं (उदाहरण के लिए,), तो आपको दूसरी विधि का सहारा लेना होगा।

दूसरी अनुवाद विधि

दूसरी विधि किसी कॉलम में या कैलकुलेटर पर अंश को हर से विभाजित करना है। संपूर्ण भाग, यदि कोई हो, परिवर्तन में भाग नहीं लेता है।

दीर्घ विभाजन का नियम जिसके परिणामस्वरूप दशमलव भिन्न प्राप्त होता है, नीचे वर्णित है (दशमलव का विभाजन देखें)।

दशमलव भिन्न को सामान्य भिन्न में बदलना

ऐसा करने के लिए, आपको इसके भिन्नात्मक भाग (दशमलव बिंदु के दाईं ओर) को अंश के रूप में लिखना चाहिए, और भिन्नात्मक भाग को पढ़ने के परिणाम को हर में संबंधित संख्या के रूप में लिखना चाहिए। अगला, यदि संभव हो तो, आपको परिणामी अंश को कम करने की आवश्यकता है।

परिमित और अनंत दशमलव भिन्न

दशमलव भिन्न को अंतिम भिन्न कहा जाता है, जिसके भिन्नात्मक भाग में अंकों की एक सीमित संख्या होती है।

उपरोक्त सभी उदाहरणों में अंतिम दशमलव भिन्न शामिल हैं। हालाँकि, प्रत्येक साधारण भिन्न को अंतिम दशमलव के रूप में प्रदर्शित नहीं किया जा सकता है। यदि पहली रूपांतरण विधि किसी दिए गए अंश के लिए लागू नहीं है, और दूसरी विधि दर्शाती है कि विभाजन पूरा नहीं किया जा सकता है, तो केवल एक अनंत दशमलव अंश प्राप्त किया जा सकता है।

किसी अनंत भिन्न को पूर्ण रूप में लिखना असंभव है। अपूर्ण रूप में, ऐसे अंशों का प्रतिनिधित्व किया जा सकता है:

1. दशमलव स्थानों की वांछित संख्या में कमी के परिणामस्वरूप;
2. एक आवधिक अंश के रूप में.

एक अंश को आवधिक कहा जाता है यदि दशमलव बिंदु के बाद अंकों के अंतहीन दोहराव वाले अनुक्रम को अलग करना संभव हो।

शेष भिन्नों को अआवधिक कहा जाता है। गैर-आवधिक भिन्नों के लिए, निरूपण की केवल पहली विधि (गोलीकरण) की अनुमति है।

आवधिक अंश का एक उदाहरण: 0.8888888... यहां एक दोहराई जाने वाली संख्या 8 है, जो, जाहिर है, अनंत काल तक दोहराई जाएगी, क्योंकि अन्यथा मानने का कोई कारण नहीं है। इस आकृति को कहा जाता है अंश की अवधि.

आवधिक अंश शुद्ध या मिश्रित हो सकते हैं। शुद्ध दशमलव अंश वह होता है जिसकी अवधि दशमलव बिंदु के तुरंत बाद शुरू होती है। मिश्रित भिन्न में दशमलव बिंदु से पहले 1 या अधिक अंक होते हैं।

54.33333… - आवधिक शुद्ध दशमलव अंश

2.562121212121… - आवधिक मिश्रित अंश

अनंत दशमलव भिन्न लिखने के उदाहरण:

दूसरा उदाहरण दिखाता है कि आवधिक अंश लिखने में अवधि को सही ढंग से कैसे प्रारूपित किया जाए।

आवधिक दशमलव भिन्नों को साधारण भिन्नों में परिवर्तित करना

एक शुद्ध आवर्त भिन्न को सामान्य आवर्त में बदलने के लिए, इसे अंश में लिखें, और आवर्त में अंकों की संख्या के बराबर मात्रा में नौ से बनी एक संख्या को हर में लिखें।

मिश्रित आवधिक दशमलव अंश का अनुवाद इस प्रकार किया गया है:

1. आपको अवधि और पहली अवधि से पहले दशमलव बिंदु के बाद की संख्या से मिलकर एक संख्या बनाने की आवश्यकता है;
2. परिणामी संख्या से, अवधि से पहले दशमलव बिंदु के बाद की संख्या घटाएं। परिणाम सामान्य भिन्न का अंश होगा;
3. हर में आपको अवधि के अंकों की संख्या के बराबर नौ की संख्या से युक्त एक संख्या दर्ज करने की आवश्यकता होती है, जिसके बाद शून्य होता है, जिसकी संख्या 1 से पहले दशमलव बिंदु के बाद संख्या के अंकों की संख्या के बराबर होती है अवधि।

दशमलव की तुलना

दशमलव भिन्नों की तुलना प्रारंभ में उनके संपूर्ण भागों से की जाती है। जिस भिन्न का पूरा भाग बड़ा होता है वह बड़ा होता है।

यदि पूर्णांक भाग समान हैं, तो पहले (दसवें से) से प्रारंभ करते हुए भिन्नात्मक भाग के संगत अंकों के अंकों की तुलना करें। वही सिद्धांत यहां लागू होता है: बड़ा अंश वह होता है जिसका दसवां हिस्सा अधिक होता है; यदि दसवां अंक बराबर है, तो सौवें अंक की तुलना की जाती है, इत्यादि।

क्योंकि

, चूंकि समान पूर्ण भागों और भिन्नात्मक भाग में समान दसवें भाग के साथ, दूसरे भिन्न में बड़ा सौवां अंक होता है।

दशमलव को जोड़ना और घटाना

दशमलव को पूर्ण संख्याओं की तरह ही एक दूसरे के नीचे संगत अंक लिखकर जोड़ा और घटाया जाता है। ऐसा करने के लिए, आपके पास दशमलव बिंदु एक दूसरे के नीचे होने चाहिए। तब पूर्णांक भाग की इकाइयाँ (दहाई, आदि), साथ ही भिन्नात्मक भाग का दसवां (सैकड़ा, आदि) तदनुसार होंगी। भिन्नात्मक भाग के लुप्त अंक शून्य से भरे जाते हैं। सीधे जोड़ और घटाव की प्रक्रिया पूर्णांकों की तरह ही की जाती है।

दशमलव को गुणा करना

दशमलव को गुणा करने के लिए, आपको उन्हें एक के नीचे एक लिखना होगा, अंतिम अंक के साथ संरेखित करना होगा और दशमलव बिंदुओं के स्थान पर ध्यान नहीं देना होगा। फिर आपको संख्याओं को उसी तरह गुणा करना होगा जैसे पूर्ण संख्याओं को गुणा करते समय करते हैं। परिणाम प्राप्त करने के बाद, आपको दोनों अंशों में दशमलव बिंदु के बाद अंकों की संख्या की पुनर्गणना करनी चाहिए और परिणामी संख्या में भिन्नात्मक अंकों की कुल संख्या को अल्पविराम से अलग करना चाहिए। यदि पर्याप्त अंक नहीं हैं, तो उन्हें शून्य से बदल दिया जाता है।

दशमलव को 10n से गुणा और विभाजित करना

ये क्रियाएं सरल हैं और दशमलव बिंदु को हिलाने तक सीमित हैं। पी गुणा करते समय, दशमलव बिंदु को 10n में शून्य की संख्या के बराबर अंकों की संख्या से दाईं ओर ले जाया जाता है (अंश बढ़ जाता है), जहां n एक मनमाना पूर्णांक घात है। अर्थात् अंकों की एक निश्चित संख्या को भिन्नात्मक भाग से पूर्ण भाग में स्थानांतरित किया जाता है। विभाजित करते समय, तदनुसार, अल्पविराम बाईं ओर चला जाता है (संख्या घट जाती है), और कुछ अंक पूर्णांक भाग से भिन्नात्मक भाग में स्थानांतरित हो जाते हैं। यदि स्थानांतरित करने के लिए पर्याप्त संख्याएँ नहीं हैं, तो गायब बिट्स शून्य से भर दिए जाते हैं।

एक दशमलव और एक पूर्ण संख्या को एक पूर्ण संख्या और एक दशमलव से विभाजित करना

दशमलव को पूर्णांक से विभाजित करना दो पूर्णांकों को विभाजित करने के समान है। इसके अतिरिक्त, आपको केवल दशमलव बिंदु की स्थिति को ध्यान में रखना होगा: किसी स्थान के अंक के बाद अल्पविराम को हटाते समय, आपको उत्पन्न उत्तर के वर्तमान अंक के बाद अल्पविराम लगाना होगा। इसके बाद आपको तब तक विभाजित करना जारी रखना होगा जब तक आपको शून्य न मिल जाए। यदि लाभांश में पूर्ण विभाजन के लिए पर्याप्त चिह्न नहीं हैं, तो उनके रूप में शून्य का उपयोग किया जाना चाहिए।

इसी प्रकार, यदि लाभांश के सभी अंक हटा दिए जाएं और पूरा विभाजन अभी तक पूरा नहीं हुआ है, तो 2 पूर्णांकों को एक कॉलम में विभाजित किया जाता है। इस मामले में, लाभांश के अंतिम अंक को हटाने के बाद, परिणामी उत्तर में एक दशमलव बिंदु रखा जाता है, और शून्य को हटाए गए अंकों के रूप में उपयोग किया जाता है। वे। यहां लाभांश अनिवार्य रूप से शून्य भिन्नात्मक भाग के साथ दशमलव अंश के रूप में दर्शाया गया है।

किसी दशमलव अंश (या पूर्णांक) को दशमलव संख्या से विभाजित करने के लिए, आपको लाभांश और भाजक को संख्या 10 n से गुणा करना होगा, जिसमें शून्य की संख्या भाजक में दशमलव बिंदु के बाद अंकों की संख्या के बराबर होती है। इस तरह, आप जिस भिन्न से भाग देना चाहते हैं उसमें दशमलव बिंदु से छुटकारा मिल जाता है। इसके अलावा, विभाजन प्रक्रिया ऊपर वर्णित प्रक्रिया से मेल खाती है।

दशमलव का चित्रमय प्रतिनिधित्व

दशमलव अंशों को एक समन्वय रेखा का उपयोग करके ग्राफ़िक रूप से दर्शाया जाता है। ऐसा करने के लिए, अलग-अलग खंडों को 10 बराबर भागों में विभाजित किया जाता है, जैसे एक रूलर पर सेंटीमीटर और मिलीमीटर को एक साथ चिह्नित किया जाता है। यह सुनिश्चित करता है कि दशमलव सटीक रूप से प्रदर्शित किए गए हैं और उनकी तुलना वस्तुनिष्ठ रूप से की जा सकती है।

एकल खंडों पर विभाजन समान होने के लिए, आपको सावधानीपूर्वक एकल खंड की लंबाई पर विचार करना चाहिए। यह ऐसा होना चाहिए जिससे अतिरिक्त विभाजन की सुविधा सुनिश्चित हो सके।

भिन्नों को 0.8 के रूप में लिखा जाता है; 0.13; 2.856; 5.2; 0.04 को दशमलव कहा जाता है. वास्तव में, दशमलव साधारण भिन्नों के लिए एक सरलीकृत अंकन है। यह अंकन उन सभी भिन्नों के लिए उपयोग करने के लिए सुविधाजनक है जिनके हर 10, 100, 1000, इत्यादि हैं।

आइए उदाहरण देखें (0.5 को शून्य दशमलव पाँच पढ़ा जाता है);

(0.15 इस प्रकार पढ़ें, शून्य दशमलव पंद्रह);

(5.3 इस प्रकार पढ़ें, पाँच दशमलव तीन)।

कृपया ध्यान दें कि दशमलव भिन्न के अंकन में, अल्पविराम किसी संख्या के पूर्णांक भाग को भिन्नात्मक भाग से अलग करता है, उचित भिन्न का पूर्णांक भाग 0 होता है। दशमलव भिन्न के भिन्नात्मक भाग के अंकन में उतने ही अंक होते हैं जितने संगत साधारण भिन्न के हर के अंकन में शून्य होते हैं।

आइए एक उदाहरण देखें, , , .

कुछ मामलों में, किसी प्राकृतिक संख्या को दशमलव मानना ​​आवश्यक हो सकता है जिसका भिन्नात्मक भाग शून्य है। यह लिखने की प्रथा है कि 5 = 5.0; 245 = 245.0 इत्यादि। ध्यान दें कि किसी प्राकृतिक संख्या के दशमलव अंकन में, सबसे कम महत्वपूर्ण अंक की इकाई आसन्न सबसे महत्वपूर्ण अंक की इकाई से 10 गुना कम होती है। यही गुण दशमलव भिन्न लिखने पर भी लागू होता है। इसलिए, दशमलव बिंदु के तुरंत बाद दसवां स्थान होता है, फिर सौवां स्थान होता है, फिर हज़ारवां स्थान होता है, इत्यादि। नीचे संख्या 31.85431 के अंकों के नाम दिए गए हैं, पहले दो स्तंभ पूर्णांक भाग हैं, शेष स्तंभ भिन्नात्मक भाग हैं।

यह अंश इकतीस दशमलव पचासी हजार चार सौ इकतीस सौ हजारवां पढ़ा जाता है।

दशमलव को जोड़ना और घटाना

पहला तरीका दशमलव भिन्नों को साधारण भिन्नों में बदलना और जोड़ करना है।

जैसा कि उदाहरण से देखा जा सकता है, यह विधि बहुत असुविधाजनक है और दशमलव अंशों को सामान्य अंशों में परिवर्तित किए बिना, दूसरी विधि का उपयोग करना बेहतर है, जो अधिक सही है। दो दशमलव भिन्नों को जोड़ने के लिए, आपको यह करना होगा:

• पदों में दशमलव बिंदु के बाद अंकों की संख्या को बराबर करना;
• पदों को एक के नीचे एक लिखें ताकि दूसरे पद का प्रत्येक अंक पहले पद के संगत अंक के नीचे हो;
• परिणामी संख्याओं को उसी प्रकार जोड़ें जैसे आप प्राकृतिक संख्याओं को जोड़ते हैं;
• पदों में अल्पविराम के नीचे परिणामी योग में अल्पविराम लगाएं।

आइए उदाहरण देखें:

• मिनटेंड और सबट्रेंड में दशमलव बिंदु के बाद अंकों की संख्या को बराबर करना;
• सबट्रेंड को मीनूएंड के नीचे लिखें ताकि सबट्रेंड का प्रत्येक अंक मीनूएंड के संबंधित अंक के अंतर्गत हो;
• घटाव उसी प्रकार करें जैसे प्राकृतिक संख्याओं को घटाया जाता है;
• मीनूएंड और सबट्रैहेंड में अल्पविराम के नीचे परिणामी अंतर में अल्पविराम लगाएं।

आइए उदाहरण देखें:

ऊपर चर्चा किए गए उदाहरणों में, यह देखा जा सकता है कि दशमलव अंशों का जोड़ और घटाव थोड़ा-थोड़ा करके किया गया था, अर्थात, उसी तरह जैसे हमने प्राकृतिक संख्याओं के साथ समान संचालन किया था। भिन्नों को दशमलव रूप में लिखने का यह मुख्य लाभ है।

दशमलव को गुणा करना

किसी दशमलव भिन्न को 10, 100, 1000 इत्यादि से गुणा करने के लिए, आपको इस भिन्न में दशमलव बिंदु को क्रमशः 1, 2, 3 इत्यादि से दाईं ओर ले जाना होगा। इसलिए, यदि अल्पविराम को 1, 2, 3 और इसी तरह के अंकों से दाईं ओर ले जाया जाता है, तो अंश तदनुसार 10, 100, 1000 और इसी तरह कई गुना बढ़ जाएगा। दो दशमलव भिन्नों को गुणा करने के लिए, आपको यह करना होगा:

• अल्पविरामों को अनदेखा करते हुए, उन्हें प्राकृतिक संख्याओं के रूप में गुणा करें;
• परिणामी उत्पाद में, दाईं ओर उतने अंकों को अल्पविराम से अलग करें, जितने दोनों कारकों में अल्पविराम के बाद होते हैं।

ऐसे मामले होते हैं जब किसी उत्पाद में अल्पविराम से अलग किए जाने की आवश्यकता से कम अंक होते हैं; इस उत्पाद से पहले बाईं ओर शून्य की आवश्यक संख्या जोड़ दी जाती है, और फिर अंकों की आवश्यक संख्या से अल्पविराम को बाईं ओर ले जाया जाता है।

आइए उदाहरण देखें: 2 * 4 = 8, फिर 0.2 * 0.4 = 0.08; 23 * 35 = 805, फिर 0.023 * 0.35 = 0.00805।

ऐसे मामले हैं जब गुणकों में से एक 0.1 के बराबर है; 0.01; 0.001 और इसी तरह, निम्नलिखित नियम का उपयोग करना अधिक सुविधाजनक है।

• दशमलव को 0.1 से गुणा करने के लिए; 0.01; 0.001 और इसी तरह, इस दशमलव अंश में आपको दशमलव बिंदु को क्रमशः 1, 2, 3, और इसी तरह बाईं ओर ले जाना होगा।

आइए उदाहरण देखें: 2.65 * 0.1 = 0.265; 457.6 * 0.01 = 4.576.

प्राकृतिक संख्याओं के गुणन के गुण दशमलव भिन्नों पर भी लागू होते हैं।

• अब = बा- गुणन की क्रमविनिमेय संपत्ति;
• (एबी) सी = ए (बीसी)- गुणन की साहचर्य संपत्ति;
• ए (बी + सी) = एबी + एसीजोड़ के सापेक्ष गुणन का एक वितरणात्मक गुण है।

दशमलव विभाजन

यह ज्ञात है कि यदि आप किसी प्राकृत संख्या को विभाजित करते हैं एएक प्राकृतिक संख्या के लिए बीऐसी प्राकृत संख्या ज्ञात करना सी, जिसे जब गुणा किया जाता है बीएक नंबर देता है ए. यदि कम से कम एक संख्या हो तो यह नियम सत्य रहता है ए, बी, सीएक दशमलव अंश है.

आइए एक उदाहरण देखें: आपको अल्पविराम को अनदेखा करते हुए, एक कोने से 43.52 को 17 से विभाजित करना होगा। इस मामले में, लाभांश में दशमलव बिंदु का उपयोग करने के बाद भागफल में अल्पविराम को पहले अंक से तुरंत पहले रखा जाना चाहिए।

ऐसे मामले होते हैं जब लाभांश भाजक से कम होता है, तो भागफल का पूर्णांक भाग शून्य के बराबर होता है। आइए एक उदाहरण देखें:

आइए एक और दिलचस्प उदाहरण देखें.

विभाजन की प्रक्रिया रुक गई है क्योंकि लाभांश के अंक समाप्त हो गए हैं और शेष में शून्य नहीं है। यह ज्ञात है कि दशमलव अंश में दाईं ओर कोई भी संख्या में शून्य जोड़ने पर कोई परिवर्तन नहीं होगा। तब यह स्पष्ट हो जाता है कि लाभांश की संख्या समाप्त नहीं हो सकती।

किसी दशमलव भिन्न को 10, 100, 1000, इत्यादि से विभाजित करने के लिए, आपको इस भिन्न में दशमलव बिंदु को 1, 2, 3, इत्यादि अंकों से बाईं ओर ले जाना होगा। आइए एक उदाहरण देखें: 5.14: 10 = 0.514; 2: 100 = 0.02; 37.51: 1000 = 0.03751.

यदि लाभांश और भाजक को एक साथ 10, 100, 1000, इत्यादि कई बार बढ़ाया जाए, तो भागफल नहीं बदलेगा।

एक उदाहरण पर विचार करें: 39.44: 1.6 = 24.65, लाभांश और भाजक को 10 गुना बढ़ाएँ 394.4: 16 = 24.65 यह ध्यान रखना उचित है कि दूसरे उदाहरण में दशमलव अंश को प्राकृतिक संख्या से विभाजित करना आसान है।

दशमलव अंश को दशमलव से विभाजित करने के लिए, आपको यह करना होगा:

• लाभांश और भाजक में अल्पविरामों को उतने अंकों तक दाईं ओर ले जाएँ जितने कि भाजक में दशमलव बिंदु के बाद होते हैं;
• एक प्राकृतिक संख्या से विभाजित करें.

आइए एक उदाहरण पर विचार करें: 23.6: 0.02, ध्यान दें कि भाजक में दो दशमलव स्थान हैं, इसलिए हम दोनों संख्याओं को 100 से गुणा करते हैं और 2360: 2 = 1180 प्राप्त करते हैं, परिणाम को 100 से विभाजित करते हैं और उत्तर प्राप्त करते हैं 11.80 या 23.6: 0, 02 = 11.8.

दशमलव की तुलना

दशमलव की तुलना करने के दो तरीके हैं। विधि एक, आपको दो दशमलव अंशों 4.321 और 4.32 की तुलना करने की आवश्यकता है, दशमलव स्थानों की संख्या को बराबर करें और स्थान दर स्थान, दसवें को दसवें के साथ, सौवें को सौवें के साथ तुलना करना शुरू करें, और इसी तरह, अंत में हमें 4.321 > 4.320 मिलता है।

दशमलव भिन्नों की तुलना करने का दूसरा तरीका गुणन का उपयोग करके किया जाता है; उपरोक्त उदाहरण को 1000 से गुणा करें और 4321 > 4320 की तुलना करें। कौन सी विधि अधिक सुविधाजनक है, हर कोई अपने लिए चुनता है।

वापस करना