สิบในเศษส่วนทศนิยมอยู่ที่ไหน? เศษส่วนทศนิยมและการดำเนินการกับพวกมัน

เศษส่วนร่วม (หรือจำนวนคละ) ซึ่งมีตัวส่วนเป็นหนึ่งตามด้วยศูนย์ตั้งแต่หนึ่งตัวขึ้นไป (เช่น 10, 100, 1000 เป็นต้น):

สามารถเขียนในรูปแบบที่ง่ายกว่า: โดยไม่ต้องใช้ตัวส่วนโดยแยกจำนวนเต็มและเศษส่วนออกจากกันด้วยลูกน้ำ (ในกรณีนี้ถือว่าส่วนจำนวนเต็มของเศษส่วนแท้เท่ากับ 0) ขั้นแรกให้เขียนทั้งส่วนจากนั้นจึงใส่ลูกน้ำและหลังจากนั้นก็เขียนส่วนที่เป็นเศษส่วน:

เศษส่วนสามัญ (หรือจำนวนคละ) ที่เขียนในรูปแบบนี้เรียกว่า ทศนิยม.

การอ่านและการเขียนทศนิยม

เศษส่วนทศนิยมเขียนตามกฎเดียวกันกับที่ใช้เขียนตัวเลขธรรมชาติในระบบเลขฐานสิบ ซึ่งหมายความว่าในรูปแบบทศนิยม เช่นเดียวกับตัวเลขธรรมชาติ แต่ละหลักจะแสดงหน่วยที่ใหญ่กว่าหน่วยที่อยู่ใกล้เคียงทางด้านขวาถึงสิบเท่า

พิจารณารายการต่อไปนี้:

เลข 8 หมายถึง หน่วยเฉพาะ เลข 3 หมายถึง หน่วยที่เล็กกว่าหน่วยธรรมดาถึง 10 เท่า เช่น สิบ 4 หมายถึง หนึ่งในร้อย 2 หมายถึง หนึ่งในพัน ฯลฯ

เรียกตัวเลขที่ปรากฏทางด้านขวาหลังจุดทศนิยม ทศนิยม.

เศษส่วนทศนิยมอ่านได้ดังนี้: ขั้นแรกให้เรียกส่วนทั้งหมดแล้วจึงเรียกส่วนที่เป็นเศษส่วน เมื่ออ่านทั้งภาคควรตอบคำถามเสมอว่าภาคทั้งหมดมีกี่หน่วย? - คำว่าทั้งหมด (หรือจำนวนเต็ม) จะถูกเพิ่มเข้าไปในคำตอบ ขึ้นอยู่กับจำนวนหน่วยทั้งหมด ตัวอย่างเช่นจำนวนเต็มหนึ่งจำนวนเต็มสองจำนวนเต็มสาม ฯลฯ เมื่ออ่านเศษส่วนจะมีการเรียกจำนวนหุ้นและในตอนท้ายพวกเขาจะเพิ่มชื่อของส่วนแบ่งเหล่านั้นซึ่งส่วนท้ายของเศษส่วนจะสิ้นสุด:

3.1 อ่านดังนี้: สามจุดหนึ่ง

2.017 อ่านได้ดังนี้ สองจุดหนึ่งหมื่นเจ็ดพัน

เพื่อให้เข้าใจกฎการเขียนและการอ่านเศษส่วนทศนิยมได้ดีขึ้น ให้พิจารณาตารางตัวเลขและตัวอย่างการเขียนตัวเลขที่ให้ไว้:

โปรดทราบว่าหลังจุดทศนิยม จะมีตัวเลขหลังจุดทศนิยมเท่ากับจำนวนศูนย์ในตัวส่วนของเศษส่วนสามัญที่สอดคล้องกัน:

ในบทช่วยสอนนี้ เราจะดูการดำเนินการแต่ละรายการแยกกัน

เนื้อหาบทเรียน

การบวกทศนิยม

ดังที่เราทราบ เศษส่วนทศนิยมมีทั้งจำนวนเต็มและเศษส่วน เมื่อบวกทศนิยม ส่วนทั้งหมดและเศษส่วนจะถูกบวกแยกกัน

ตัวอย่างเช่น ลองบวกเศษส่วนทศนิยม 3.2 และ 5.3 การบวกเศษส่วนทศนิยมในคอลัมน์จะสะดวกกว่า

ก่อนอื่น เรามาเขียนเศษส่วนทั้งสองนี้ในคอลัมน์เดียวกัน โดยส่วนที่เป็นจำนวนเต็มจะต้องอยู่ใต้จำนวนเต็ม และเศษส่วนอยู่ใต้เศษส่วน ที่โรงเรียนเราเรียกข้อกำหนดนี้ว่า "ลูกน้ำใต้ลูกน้ำ".

ลองเขียนเศษส่วนลงในคอลัมน์โดยให้ลูกน้ำอยู่ใต้ลูกน้ำ:

เราเริ่มบวกเศษส่วน: 2 + 3 = 5 เราเขียนห้าในส่วนที่เป็นเศษส่วนของคำตอบ:

ตอนนี้เรารวมส่วนทั้งหมดเข้าด้วยกัน: 3 + 5 = 8 เราเขียนแปดในส่วนทั้งหมดของคำตอบ:

ตอนนี้เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้เราปฏิบัติตามกฎอีกครั้ง "ลูกน้ำใต้ลูกน้ำ":

เราได้รับคำตอบ 8.5 ดังนั้นนิพจน์ 3.2 + 5.3 เท่ากับ 8.5

ที่จริงแล้วไม่ใช่ทุกอย่างจะง่ายอย่างที่คิดเมื่อเห็นแวบแรก นอกจากนี้ยังมีข้อผิดพลาดที่นี่ซึ่งเราจะพูดถึงตอนนี้

ตำแหน่งเป็นทศนิยม

เศษส่วนทศนิยมก็เหมือนกับตัวเลขทั่วไปที่มีตัวเลขเป็นของตัวเอง เหล่านี้เป็นสถานที่ที่สิบ, ที่ร้อย, ที่หนึ่งในพัน. ในกรณีนี้ ตัวเลขจะเริ่มต้นหลังจุดทศนิยม

หลักแรกหลังจุดทศนิยมคือหลักสิบ หลักที่สองหลังจุดทศนิยมคือหลักร้อย และหลักที่สามหลังจุดทศนิยมคือหลักพัน

ตำแหน่งทศนิยมประกอบด้วยข้อมูลที่เป็นประโยชน์บางประการ โดยเฉพาะอย่างยิ่ง พวกเขาบอกคุณว่ามีทศนิยมกี่ในสิบ ร้อย และหนึ่งในพัน

เช่น พิจารณาเศษส่วนทศนิยม 0.345

ตำแหน่งที่ทั้งสามตั้งอยู่นั้นเรียกว่า อันดับที่สิบ

ตำแหน่งที่ทั้งสี่ตั้งอยู่เรียกว่า อันดับที่ร้อย

ตำแหน่งที่ทั้งห้าตั้งอยู่เรียกว่า อันดับที่พัน

ลองดูภาพวาดนี้ เราเห็นว่ามีสามอยู่ในตำแหน่งที่สิบ. ซึ่งหมายความว่ามีสามในสิบของเศษส่วนทศนิยม 0.345

ถ้าเราบวกเศษส่วน เราจะได้เศษส่วนทศนิยมเดิม 0.345

จะเห็นได้ว่าตอนแรกเราได้คำตอบแต่เราแปลงเป็นเศษส่วนทศนิยมแล้วได้ 0.345

เมื่อบวกเศษส่วนทศนิยม จะต้องปฏิบัติตามหลักการและกฎเดียวกันกับเมื่อบวกเลขธรรมดา การบวกเศษส่วนทศนิยมเกิดขึ้นในหลัก: ส่วนที่สิบจะถูกบวกเข้ากับหลักสิบ, หลักร้อยถึงหลักร้อย, หลักพันถึงหลักพัน

ดังนั้นเมื่อบวกเศษส่วนทศนิยมจึงต้องปฏิบัติตามกฎ "ลูกน้ำใต้ลูกน้ำ"- เครื่องหมายจุลภาคใต้เครื่องหมายจุลภาคระบุลำดับของการบวกหนึ่งในสิบเข้ากับสิบ, ในร้อยถึงหลักร้อย, ในพันถึงในพัน

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 1.5 + 3.4

ก่อนอื่น เราบวกเศษส่วน 5 + 4 = 9 เราเขียนเก้าไว้ในส่วนของเศษส่วนของคำตอบ:

ตอนนี้เราบวกจำนวนเต็มส่วนที่ 1 + 3 = 4 เราเขียนสี่ในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค ในการดำเนินการนี้ ให้ปฏิบัติตามกฎ "ลูกน้ำใต้ลูกน้ำ" อีกครั้ง:

เราได้รับคำตอบ 4.9 ซึ่งหมายความว่าค่าของนิพจน์ 1.5 + 3.4 คือ 4.9

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์: 3.51 + 1.22

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ"

ก่อนอื่น เราบวกเศษส่วนเข้าด้วยกัน ซึ่งก็คือส่วนในร้อยของ 1+2=3 เราเขียนคำตอบสามเท่าในส่วนที่ร้อย:

ตอนนี้บวกส่วนที่สิบ 5+2=7 เราเขียนเจ็ดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราบวกทั้งส่วน 3+1=4 เราเขียนทั้งสี่ในส่วนทั้งหมดของคำตอบของเรา:

เราแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ โดยปฏิบัติตามกฎ "ลูกน้ำใต้ลูกน้ำ":

คำตอบที่เราได้รับคือ 4.73 ซึ่งหมายความว่าค่าของนิพจน์ 3.51 + 1.22 เท่ากับ 4.73

3,51 + 1,22 = 4,73

เช่นเดียวกับตัวเลขทั่วไป เมื่อบวกทศนิยม . ในกรณีนี้คำตอบจะเขียนหนึ่งหลักและส่วนที่เหลือจะถูกโอนไปยังหลักถัดไป

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 2.65 + 3.27

เราเขียนนิพจน์นี้ลงในคอลัมน์:

เพิ่มส่วนที่ร้อย 5+7=12 หมายเลข 12 จะไม่พอดีกับส่วนที่ร้อยของคำตอบของเรา ดังนั้นในส่วนที่ร้อยเราจึงเขียนเลข 2 และย้ายหน่วยไปที่หลักถัดไป:

ตอนนี้เราบวกหนึ่งในสิบของ 6+2=8 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 9 เราเขียนเลข 9 ในส่วนที่สิบของคำตอบ:

ตอนนี้เราบวกทั้งส่วน 2+3=5 เราเขียนเลข 5 ไว้ในส่วนจำนวนเต็มของคำตอบ:

เราได้รับคำตอบ 5.92 ซึ่งหมายความว่าค่าของนิพจน์ 2.65 + 3.27 เท่ากับ 5.92

2,65 + 3,27 = 5,92

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ 9.5 + 2.8

เราเขียนนิพจน์นี้ลงในคอลัมน์

เราบวกเศษส่วน 5 + 8 = 13 ตัวเลข 13 จะไม่พอดีกับเศษส่วนของคำตอบ ดังนั้นเราจึงเขียนเลข 3 ก่อนแล้วย้ายหน่วยไปที่หลักถัดไป หรือโอนไปที่ ส่วนจำนวนเต็ม:

ตอนนี้เราบวกส่วนจำนวนเต็ม 9+2=11 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 12 เราเขียนเลข 12 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 12.3. ซึ่งหมายความว่าค่าของนิพจน์ 9.5 + 2.8 คือ 12.3

9,5 + 2,8 = 12,3

เมื่อบวกทศนิยม จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองจะต้องเท่ากัน หากมีตัวเลขไม่เพียงพอ สถานที่เหล่านี้ในส่วนเศษส่วนจะเต็มไปด้วยศูนย์

ตัวอย่างที่ 5- ค้นหาค่าของนิพจน์: 12.725 + 1.7

ก่อนที่จะเขียนนิพจน์นี้ในคอลัมน์ เรามาทำให้จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองเท่ากันก่อน เศษส่วนทศนิยม 12.725 มีเลขสามหลักหลังจุดทศนิยม แต่เศษส่วน 1.7 มีเพียงเลขเดียว ซึ่งหมายความว่าในส่วน 1.7 คุณต้องเพิ่มศูนย์สองตัวต่อท้าย แล้วเราจะได้เศษส่วน 1.700. ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์และเริ่มคำนวณได้:

บวกส่วนที่พัน 5+0=5 เราเขียนเลข 5 ในส่วนหนึ่งในพันของคำตอบ:

เพิ่มส่วนที่ร้อย 2+0=2 เราเขียนหมายเลข 2 ในส่วนที่ร้อยของคำตอบ:

บวกส่วนสิบ 7+7=14 หมายเลข 14 จะไม่พอดีกับหนึ่งในสิบของคำตอบของเรา ดังนั้นเราจึงเขียนเลข 4 ก่อนแล้วเลื่อนหน่วยไปที่หลักถัดไป:

ตอนนี้เราบวกส่วนจำนวนเต็ม 12+1=13 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 14 เราเขียนเลข 14 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 14,425 คน ซึ่งหมายความว่าค่าของนิพจน์ 12.725+1.700 คือ 14.425

12,725+ 1,700 = 14,425

การลบทศนิยม

เมื่อลบเศษส่วนทศนิยม คุณต้องปฏิบัติตามกฎเดียวกันกับการบวก: “ลูกน้ำใต้จุดทศนิยม” และ “จำนวนหลักเท่ากันหลังจุดทศนิยม”

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 − 2.2

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ":

เราคำนวณเศษส่วน 5−2=3 เราเขียนหมายเลข 3 ในส่วนที่สิบของคำตอบ:

เราคำนวณจำนวนเต็มส่วนที่ 2−2=0 เราเขียนศูนย์ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 0.3 ซึ่งหมายความว่าค่าของนิพจน์ 2.5 - 2.2 เท่ากับ 0.3

2,5 − 2,2 = 0,3

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 7.353 - 3.1

นิพจน์นี้มีทศนิยมจำนวนต่างกัน เศษส่วน 7.353 มีเลขสามหลักหลังจุดทศนิยม แต่เศษส่วน 3.1 มีเพียงเลขเดียว ซึ่งหมายความว่าในเศษส่วน 3.1 คุณต้องเพิ่มศูนย์สองตัวต่อท้ายเพื่อทำให้จำนวนหลักในเศษส่วนทั้งสองเท่ากัน แล้วเราจะได้ 3,100.

ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์แล้วคำนวณได้:

เราได้รับคำตอบ 4,253 คน ซึ่งหมายความว่าค่าของนิพจน์ 7.353 − 3.1 เท่ากับ 4.253

7,353 — 3,1 = 4,253

เช่นเดียวกับตัวเลขทั่วไป บางครั้งคุณจะต้องยืมเลขหนึ่งจากเลขหลักที่อยู่ติดกันหากการลบเป็นไปไม่ได้

ตัวอย่างที่ 3จงหาค่าของนิพจน์ 3.46 − 2.39

ลบหนึ่งในร้อยของ 6−9 คุณไม่สามารถลบเลข 9 จากเลข 6 ได้ ดังนั้นคุณต้องยืมเลขหนึ่งจากเลขหลักที่อยู่ติดกัน โดยการยืมหนึ่งจากหลักที่อยู่ติดกัน เลข 6 จะกลายเป็นเลข 16 ตอนนี้คุณสามารถคำนวณหนึ่งในร้อยของ 16−9=7 ได้ เราเขียนคำตอบเจ็ดส่วนในร้อย:

ตอนนี้เราลบสิบ. เนื่องจากเราได้หนึ่งหน่วยในอันดับที่สิบ จำนวนตัวเลขที่อยู่ตรงนั้นจึงลดลงหนึ่งหน่วย กล่าวอีกนัยหนึ่ง ในอันดับที่สิบตอนนี้ไม่ใช่เลข 4 แต่เป็นเลข 3 ลองคำนวณหนึ่งในสิบของ 3−3=0 กัน เราเขียนศูนย์ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราลบส่วนทั้งหมด 3−2=1 เราเขียนไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้รับคำตอบ 1.07 ซึ่งหมายความว่าค่าของนิพจน์ 3.46−2.39 เท่ากับ 1.07

3,46−2,39=1,07

ตัวอย่างที่ 4- ค้นหาค่าของนิพจน์ 3−1.2

ตัวอย่างนี้จะลบทศนิยมจากจำนวนเต็ม ลองเขียนนิพจน์นี้ลงในคอลัมน์เพื่อให้เศษส่วนทศนิยม 1.23 ทั้งหมดอยู่ใต้เลข 3

ทีนี้ลองทำให้จำนวนหลักหลังจุดทศนิยมเท่ากัน ในการทำเช่นนี้หลังจากหมายเลข 3 เราใส่เครื่องหมายจุลภาคและเพิ่มศูนย์หนึ่งตัว:

ตอนนี้เราลบสิบ: 0−2 คุณไม่สามารถลบเลข 2 จากศูนย์ได้ ดังนั้น คุณต้องยืมเลขตัวหนึ่งจากหลักที่อยู่ติดกัน เมื่อยืมมาหนึ่งตัวจากหลักข้างเคียง 0 จะเปลี่ยนเป็นเลข 10 ตอนนี้คุณสามารถคำนวณหนึ่งในสิบของ 10−2=8 ได้ เราเขียนแปดในส่วนที่สิบของคำตอบของเรา:

ตอนนี้เราลบส่วนทั้งหมดออก ก่อนหน้านี้หมายเลข 3 ตั้งอยู่ทั้งหมด แต่เราเอามาหนึ่งหน่วยจากมัน เป็นผลให้มันกลายเป็นเลข 2 ดังนั้นจาก 2 เราลบ 1 2−1=1 เราเขียนไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

คำตอบที่เราได้รับคือ 1.8 ซึ่งหมายความว่าค่าของนิพจน์ 3−1.2 คือ 1.8

การคูณทศนิยม

การคูณทศนิยมนั้นง่ายและสนุกด้วยซ้ำ หากต้องการคูณทศนิยม คุณต้องคูณมันเหมือนตัวเลขปกติ โดยไม่สนใจเครื่องหมายจุลภาค

เมื่อได้รับคำตอบแล้ว คุณจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง จากนั้นนับจำนวนหลักเท่ากันจากทางขวาในคำตอบแล้วใส่ลูกน้ำ

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 × 1.5

ลองคูณเศษส่วนทศนิยมเหมือนตัวเลขธรรมดา โดยไม่สนใจลูกน้ำ หากต้องการเพิกเฉยต่อเครื่องหมายจุลภาค คุณสามารถจินตนาการได้ว่าเครื่องหมายเหล่านั้นหายไปเลย:

เราได้ 375 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.5 และ 1.5 เศษส่วนแรกมีหนึ่งหลักหลังจุดทศนิยม และเศษส่วนที่สองก็มีหนึ่งหลักด้วย รวมสองตัวเลข

เรากลับไปที่หมายเลข 375 และเริ่มเคลื่อนจากขวาไปซ้าย เราจำเป็นต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้คำตอบ 3.75 ดังนั้นค่าของนิพจน์ 2.5 × 1.5 คือ 3.75

2.5 × 1.5 = 3.75

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 12.85 × 2.7

ลองคูณเศษส่วนทศนิยมเหล่านี้โดยไม่สนใจลูกน้ำ:

เราได้ 34695 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 12.85 และ 2.7 เศษส่วน 12.85 มีตัวเลขสองหลักหลังจุดทศนิยม และเศษส่วน 2.7 มีตัวเลขหนึ่งหลัก - รวมเป็นสามหลัก

เรากลับไปที่หมายเลข 34695 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับสามหลักจากทางขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 34,695 คน ดังนั้นค่าของนิพจน์ 12.85 × 2.7 คือ 34.695

12.85 × 2.7 = 34.695

การคูณทศนิยมด้วยจำนวนปกติ

บางครั้งสถานการณ์เกิดขึ้นเมื่อคุณต้องการคูณเศษส่วนทศนิยมด้วยจำนวนปกติ

หากต้องการคูณทศนิยมและตัวเลข คุณต้องคูณพวกมันโดยไม่ต้องสนใจเครื่องหมายจุลภาคในทศนิยม เมื่อได้รับคำตอบแล้ว คุณจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทศนิยมจากนั้นนับจำนวนหลักจากทางขวาในคำตอบแล้วใส่ลูกน้ำ

เช่น คูณ 2.54 ด้วย 2

คูณเศษส่วนทศนิยม 2.54 ด้วยตัวเลขปกติ 2 โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้หมายเลข 508 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.54 เศษส่วน 2.54 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 508 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 5.08 ดังนั้นค่าของนิพจน์ 2.54 × 2 คือ 5.08

2.54 × 2 = 5.08

การคูณทศนิยมด้วย 10, 100, 1,000

การคูณทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับการคูณทศนิยมด้วยตัวเลขปกติ คุณต้องทำการคูณโดยไม่สนใจลูกน้ำในเศษส่วนทศนิยมจากนั้นในคำตอบให้แยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนโดยนับจากทางขวาด้วยจำนวนหลักเท่ากันเนื่องจากมีตัวเลขอยู่หลังจุดทศนิยม

เช่น คูณ 2.88 ด้วย 10

คูณเศษส่วนทศนิยม 2.88 ด้วย 10 โดยไม่สนใจเครื่องหมายจุลภาคในเศษส่วนทศนิยม:

เราได้ 2880 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.88 เราจะเห็นว่าเศษส่วน 2.88 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 2880 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับตัวเลขสองหลักทางด้านขวาและใส่ลูกน้ำ:

เราได้รับคำตอบ 28.80. ลองปล่อยศูนย์สุดท้ายแล้วได้ 28.8 ซึ่งหมายความว่าค่าของนิพจน์ 2.88×10 คือ 28.8

2.88 × 10 = 28.8

มีวิธีที่สองในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยการเลื่อนจุดทศนิยมไปทางขวาตามหลักจำนวนเท่าที่มีเลขศูนย์อยู่ในตัวประกอบ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 2.88×10 ด้วยวิธีนี้ เราจะดูปัจจัย 10 ทันทีโดยไม่ต้องคำนวณใดๆ เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์หนึ่งตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เราได้ 28.8

2.88 × 10 = 28.8

ลองคูณ 2.88 ด้วย 100 ดูตัวประกอบ 100 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์สองตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาสองหลัก จะได้ 288

2.88 × 100 = 288

ลองคูณ 2.88 ด้วย 1,000 ดูตัวประกอบ 1,000 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามีศูนย์สามตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาสามหลัก ไม่มีหลักที่สามดังนั้นเราจึงบวกศูนย์อีกตัวหนึ่ง เป็นผลให้เราได้ 2880

2.88 × 1,000 = 2880

การคูณทศนิยมด้วย 0.1 0.01 และ 0.001

การคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 มีการทำงานในลักษณะเดียวกับการคูณทศนิยมด้วยทศนิยม จำเป็นต้องคูณเศษส่วนเหมือนตัวเลขธรรมดาแล้วใส่ลูกน้ำในคำตอบโดยนับหลักทางด้านขวาเท่ากับจำนวนหลักที่อยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

เช่น คูณ 3.25 ด้วย 0.1

เราคูณเศษส่วนเหล่านี้เหมือนตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 325 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 3.25 และ 0.1 เศษส่วน 3.25 มีตัวเลขสองหลักหลังจุดทศนิยม และเศษส่วน 0.1 มีตัวเลขหนึ่งหลัก รวมสามตัวเลข

เรากลับไปที่หมายเลข 325 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับสามหลักจากทางขวาและใส่ลูกน้ำ หลังจากนับถอยหลังสามหลักก็พบว่าตัวเลขหมด ในกรณีนี้ คุณต้องเพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ:

เราได้รับคำตอบ 0.325 ซึ่งหมายความว่าค่าของนิพจน์ 3.25 × 0.1 คือ 0.325

3.25 × 0.1 = 0.325

มีวิธีที่สองในการคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยการเลื่อนจุดทศนิยมไปทางซ้ายตามหลักจำนวนเท่าที่มีเลขศูนย์อยู่ในตัวประกอบ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 3.25 × 0.1 ด้วยวิธีนี้ โดยไม่ต้องคำนวณใดๆ เราจะดูตัวคูณ 0.1 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราเลื่อนจุดทศนิยมไปทางซ้ายหนึ่งหลัก โดยการเลื่อนเครื่องหมายจุลภาคไปทางซ้ายหนึ่งหลัก เราจะเห็นว่าไม่มีหลักอื่นอยู่ก่อนหลักสามหลัก ในกรณีนี้ ให้เพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ ผลลัพธ์คือ 0.325

3.25 × 0.1 = 0.325

ลองคูณ 3.25 ด้วย 0.01 กัน เราจะดูตัวคูณ 0.01 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์สองตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายสองหลัก เราได้ 0.0325

3.25 × 0.01 = 0.0325

ลองคูณ 3.25 ด้วย 0.001 กัน เราจะดูตัวคูณ 0.001 ทันที เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์สามตัวอยู่ในนั้น ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายสามหลัก เราได้ 0.00325

3.25 × 0.001 = 0.00325

อย่าสับสนระหว่างการคูณเศษส่วนทศนิยมด้วย 0.1, 0.001 และ 0.001 กับการคูณด้วย 10, 100, 1,000 ถือเป็นข้อผิดพลาดทั่วไปสำหรับคนส่วนใหญ่

เมื่อคูณด้วย 10, 100, 1,000 จุดทศนิยมจะเลื่อนไปทางขวาด้วยจำนวนหลักเท่ากันเนื่องจากมีเลขศูนย์อยู่ในตัวคูณ

และเมื่อคูณด้วย 0.1, 0.01 และ 0.001 จุดทศนิยมจะเลื่อนไปทางซ้ายด้วยจำนวนหลักเท่ากันเนื่องจากมีเลขศูนย์อยู่ในตัวคูณ

หากจำยากในตอนแรก คุณสามารถใช้วิธีแรก ซึ่งจะทำการคูณเช่นเดียวกับตัวเลขธรรมดา คำตอบจะต้องแยกส่วนทั้งหมดออกจากส่วนที่เป็นเศษส่วนโดยนับเลขหลักทางด้านขวาให้เท่ากันเนื่องจากมีเลขหลักอยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

การหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า ระดับสูง.

ในบทเรียนก่อนหน้านี้บทหนึ่ง เราบอกว่าเมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้เศษส่วนมา โดยตัวเศษคือเงินปันผล และตัวส่วนคือตัวหาร

ตัวอย่างเช่น หากต้องการแบ่งแอปเปิ้ลหนึ่งผลระหว่างสอง คุณต้องเขียน 1 (แอปเปิ้ลหนึ่งผล) ในตัวเศษ และเขียน 2 (เพื่อนสองคน) ในตัวส่วน ผลลัพธ์ที่ได้คือเศษส่วน ซึ่งหมายความว่าเพื่อนแต่ละคนจะได้รับแอปเปิ้ล กล่าวอีกนัยหนึ่งคือแอปเปิ้ลครึ่งลูก เศษส่วนคือคำตอบของปัญหา “วิธีแบ่งแอปเปิ้ลหนึ่งผลออกเป็นสองผล”

ปรากฎว่าคุณสามารถแก้ปัญหานี้ต่อไปได้หากคุณหาร 1 ด้วย 2 ท้ายที่สุดแล้ว เส้นเศษส่วนในเศษส่วนใดๆ ก็หมายถึงการหาร ดังนั้น การหารนี้จึงได้รับอนุญาตให้เป็นเศษส่วนได้ แต่อย่างไร? เราคุ้นเคยกับความจริงที่ว่าเงินปันผลจะมากกว่าตัวหารเสมอ แต่ตรงนี้ ตรงกันข้าม เงินปันผลน้อยกว่าตัวหาร.

ทุกอย่างจะชัดเจนถ้าเราจำไว้ว่าเศษส่วนหมายถึงการแตกสลาย การแบ่ง การแบ่ง ซึ่งหมายความว่าหน่วยสามารถแบ่งออกเป็นส่วนต่างๆ ได้มากเท่าที่ต้องการ ไม่ใช่แค่เพียงสองส่วนเท่านั้น

เมื่อคุณหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากขึ้น คุณจะได้เศษส่วนทศนิยมซึ่งส่วนของจำนวนเต็มคือ 0 (ศูนย์) เศษส่วนสามารถเป็นอะไรก็ได้

ลองหาร 1 ด้วย 2 กัน ลองแก้ตัวอย่างนี้ด้วยมุม:

หนึ่งไม่สามารถแบ่งออกเป็นสองอย่างสมบูรณ์ หากคุณถามคำถาม “หนึ่งมีกี่สอง” แล้วคำตอบจะเป็น 0 ดังนั้นในผลหารเราจึงเขียน 0 และใส่ลูกน้ำ:

ตามปกติแล้ว เราคูณผลหารด้วยตัวหารเพื่อให้ได้ส่วนที่เหลือ:

ถึงเวลาแล้วที่หน่วยสามารถแบ่งออกเป็นสองส่วนได้ เมื่อต้องการทำเช่นนี้ ให้เพิ่มศูนย์อีกตัวทางด้านขวาของผลลัพธ์:

เราได้ 10. หาร 10 ด้วย 2 เราได้ 5. เราเขียนห้าไว้ในส่วนของเศษส่วนของคำตอบ:

ตอนนี้เรานำส่วนที่เหลือสุดท้ายออกมาเพื่อคำนวณให้เสร็จสิ้น คูณ 5 ด้วย 2 เพื่อให้ได้ 10

เราได้รับคำตอบ 0.5 ดังนั้นเศษส่วนคือ 0.5

แอปเปิลครึ่งลูกสามารถเขียนได้โดยใช้เศษส่วนทศนิยม 0.5 หากเราเพิ่มทั้งสองซีกนี้ (0.5 และ 0.5) เราจะได้แอปเปิ้ลดั้งเดิมทั้งหมดอีกครั้ง:

ประเด็นนี้สามารถเข้าใจได้หากคุณจินตนาการว่า 1 ซม. แบ่งออกเป็นสองส่วนอย่างไร ถ้าแบ่ง 1 เซนติเมตรออกเป็น 2 ส่วน จะได้ 0.5 ซม

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 4:5

มีห้ากี่ในสี่? ไม่เลย. เราเขียน 0 ลงในผลหารและใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียนศูนย์ไว้ใต้เลขสี่. ลบศูนย์นี้ออกจากเงินปันผลทันที:

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) สี่ส่วนออกเป็น 5 ส่วนกัน เมื่อต้องการทำสิ่งนี้ ให้บวกศูนย์ทางด้านขวาของ 4 แล้วหาร 40 ด้วย 5 เราจะได้ 8 เราเขียน 8 ลงในผลหาร

เราทำตัวอย่างให้สมบูรณ์โดยการคูณ 8 ด้วย 5 เพื่อให้ได้ 40:

เราได้รับคำตอบ 0.8 ซึ่งหมายความว่าค่าของนิพจน์ 4:5 คือ 0.8

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 5: 125

125 มีกี่หมายเลขในห้า? ไม่เลย. เราเขียน 0 ลงในผลหารและใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้ห้า. ลบ 0 จากห้าทันที

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) ห้าส่วนออกเป็น 125 ส่วนกัน เมื่อต้องการทำสิ่งนี้ ให้เขียนศูนย์ทางด้านขวาของห้าค่านี้:

หาร 50 ด้วย 125 จำนวน 125 ในจำนวน 50 มีกี่หมายเลข? ไม่เลย. ในผลหารเราจึงเขียน 0 อีกครั้ง

คูณ 0 ด้วย 125 เราจะได้ 0 เขียนศูนย์นี้ไว้ใต้ 50 ลบ 0 ออกจาก 50 ทันที

ตอนนี้แบ่งจำนวน 50 ออกเป็น 125 ส่วน เมื่อต้องการทำสิ่งนี้ ให้เขียนศูนย์อีกอันทางด้านขวาของ 50:

หาร 500 ด้วย 125 จำนวน 125 ในจำนวน 500 มีกี่จำนวน 125 มีสี่จำนวนในจำนวน 500 เขียนสี่ลงในผลหาร:

เราทำตัวอย่างให้สมบูรณ์โดยคูณ 4 ด้วย 125 เพื่อให้ได้ 500

เราได้รับคำตอบ 0.04 ซึ่งหมายความว่าค่าของนิพจน์ 5: 125 คือ 0.04

การหารตัวเลขโดยไม่มีเศษ

ดังนั้น ให้ใส่ลูกน้ำหลังหน่วยในผลหาร เพื่อเป็นการระบุว่าการหารส่วนจำนวนเต็มสิ้นสุดลงแล้ว และเรากำลังดำเนินการไปยังส่วนที่เป็นเศษส่วน:

ลองบวกศูนย์เข้ากับเศษ 4 กัน

ทีนี้หาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดลงในผลหาร:

40−40=0 เราเหลือ 0 หมายความว่าการแบ่งส่วนเสร็จสมบูรณ์แล้ว การหาร 9 ด้วย 5 จะได้เศษส่วนทศนิยม 1.8:

9: 5 = 1,8

ตัวอย่างที่ 2- หาร 84 ด้วย 5 โดยไม่มีเศษ

ขั้นแรก ให้หาร 84 ด้วย 5 ตามปกติด้วยเศษ:

เราได้ 16 อันเป็นการส่วนตัว และเหลืออีก 4 อัน ทีนี้ลองหารเศษนี้ด้วย 5 ใส่ลูกน้ำในตัวผลหารแล้วบวก 0 เข้ากับเศษ 4

ทีนี้หาร 40 ด้วย 5 เราได้ 8 เราเขียนเลขแปดลงในผลหารหลังจุดทศนิยม:

และทำตัวอย่างให้สมบูรณ์โดยตรวจสอบว่ายังมีเศษเหลืออยู่หรือไม่:

การหารทศนิยมด้วยจำนวนปกติ

อย่างที่เราทราบเศษส่วนทศนิยมประกอบด้วยจำนวนเต็มและเศษส่วน เมื่อทำการหารเศษส่วนทศนิยมด้วยจำนวนปกติ สิ่งแรกที่คุณต้องทำคือ:

• หารเศษส่วนทศนิยมทั้งหมดด้วยจำนวนนี้
• หลังจากแบ่งส่วนทั้งหมดแล้วคุณจะต้องใส่ลูกน้ำในผลหารทันทีและคำนวณต่อเช่นเดียวกับในการหารปกติ

เช่น หาร 4.8 ด้วย 2

ลองเขียนตัวอย่างนี้ในมุม:

ทีนี้ลองหารทั้งหมดด้วย 2. สี่หารด้วยสองเท่ากับสอง. เราเขียนสองตัวในผลหารแล้วใส่ลูกน้ำทันที:

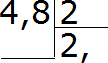
ตอนนี้เราคูณผลหารด้วยตัวหารแล้วดูว่ายังมีเศษเหลือจากการหารหรือไม่:

4−4=0 ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนเป็นศูนย์ เนื่องจากการแก้ปัญหายังไม่เสร็จสมบูรณ์ ต่อไปเราคำนวณต่อไปเหมือนการหารปกติ ถอด 8 ลงมาแล้วหารด้วย 2

8: 2 = 4 เราเขียนสี่ลงในผลหารแล้วคูณด้วยตัวหารทันที:

เราได้รับคำตอบ 2.4 ค่าของนิพจน์ 4.8:2 คือ 2.4

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 8.43: 3

หาร 8 ด้วย 3 เราได้ 2 ใส่ลูกน้ำหลัง 2 ทันที:

ตอนนี้เราคูณผลหารด้วยตัวหาร 2 × 3 = 6 เราเขียนหกไว้ใต้แปดแล้วหาเศษ:

หาร 24 ด้วย 3 เราได้ 8. เราเขียน 8 ไว้ในผลหาร. คูณด้วยตัวหารทันทีเพื่อหาเศษที่เหลือของการหาร:

24−24=0 ส่วนที่เหลือเป็นศูนย์ เรายังไม่ได้เขียนลงศูนย์เลย เรานำสามตัวสุดท้ายออกจากเงินปันผลแล้วหารด้วย 3 เราได้ 1 คูณ 1 ด้วย 3 ทันทีเพื่อทำให้ตัวอย่างนี้สมบูรณ์:

คำตอบที่เราได้รับคือ 2.81 ซึ่งหมายความว่าค่าของนิพจน์ 8.43: 3 คือ 2.81

การหารทศนิยมด้วยทศนิยม

หากต้องการหารเศษส่วนทศนิยมด้วยเศษส่วนทศนิยม คุณต้องย้ายจุดทศนิยมในตัวหารและตัวหารไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร แล้วหารด้วยจำนวนปกติ

เช่น หาร 5.95 ด้วย 1.7

ลองเขียนนิพจน์นี้ด้วยมุม

ตอนนี้ในการจ่ายเงินปันผลและในตัวหาร เราย้ายจุดทศนิยมไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ซึ่งหมายความว่าในการจ่ายเงินปันผลและตัวหารเราต้องย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เราโอน:

หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้ว เศษส่วนทศนิยม 5.95 ก็กลายเป็นเศษส่วน 59.5 และเศษส่วนทศนิยม 1.7 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักก็กลายเป็นเลขปกติ 17 และเรารู้วิธีหารเศษส่วนทศนิยมด้วยตัวเลขปกติแล้ว การคำนวณเพิ่มเติมไม่ใช่เรื่องยาก:

เครื่องหมายจุลภาคถูกย้ายไปทางขวาเพื่อให้การแบ่งง่ายขึ้น ที่อนุญาตได้เพราะเมื่อคูณหรือหารเงินปันผลและตัวหารด้วยจำนวนเดียวกัน ผลหารจะไม่เปลี่ยนแปลง มันหมายความว่าอะไร?

นี่เป็นหนึ่งในคุณสมบัติที่น่าสนใจของการแบ่ง เรียกว่าคุณสมบัติผลหาร พิจารณานิพจน์ 9: 3 = 3 หากในนิพจน์นี้เงินปันผลและตัวหารถูกคูณหรือหารด้วยจำนวนเดียวกัน ผลหาร 3 จะไม่เปลี่ยนแปลง

ลองคูณเงินปันผลและตัวหารด้วย 2 แล้วดูว่าได้อะไร:

(9 × 2) : (3 × 2) = 18: 6 = 3

ดังที่เห็นได้จากตัวอย่าง ผลหารไม่มีการเปลี่ยนแปลง

สิ่งเดียวกันนี้เกิดขึ้นเมื่อเราย้ายลูกน้ำในตัวหารและตัวหาร ในตัวอย่างก่อนหน้านี้ เราหาร 5.91 ด้วย 1.7 เราได้ย้ายเครื่องหมายจุลภาคในเงินปันผลและตัวหารไปทางขวาหนึ่งหลัก หลังจากย้ายจุดทศนิยมแล้ว เศษส่วน 5.91 ก็แปลงเป็นเศษส่วน 59.1 และเศษส่วน 1.7 ก็แปลงเป็นเลข 17 ปกติ

อันที่จริง ภายในกระบวนการนี้ มีการคูณด้วย 10 นี่คือลักษณะที่ปรากฏ:

5.91 × 10 = 59.1

ดังนั้นจำนวนหลักหลังจุดทศนิยมในตัวหารจะกำหนดว่าเงินปันผลและตัวหารจะคูณด้วยอะไร กล่าวอีกนัยหนึ่งจำนวนหลักหลังจุดทศนิยมในตัวหารจะกำหนดจำนวนหลักในการจ่ายเงินปันผลและในตัวหารจุดทศนิยมจะถูกย้ายไปทางขวา

การหารทศนิยมด้วย 10, 100, 1,000

การหารทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับ ตัวอย่างเช่น หาร 2.1 ด้วย 10 แก้ตัวอย่างนี้โดยใช้มุม:

แต่มีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกย้ายไปทางซ้ายตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 2.1: 10. เราดูตัวหาร. เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 คุณต้องเลื่อนจุดทศนิยมไปทางซ้ายหนึ่งหลัก เราเลื่อนลูกน้ำไปทางซ้ายหนึ่งหลักแล้วดูว่าไม่มีหลักเหลือแล้ว ในกรณีนี้ ให้บวกศูนย์อีกตัวก่อนตัวเลข ผลลัพธ์ที่ได้คือ 0.21

ลองหาร 2.1 ด้วย 100 กัน มีศูนย์สองตัวใน 100 ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 เราจำเป็นต้องเลื่อนลูกน้ำไปทางซ้ายสองหลัก:

2,1: 100 = 0,021

ลองหาร 2.1 ด้วย 1,000 กัน มีศูนย์สามตัวใน 1,000 ซึ่งหมายความว่าในการจ่ายเงินปันผล 2.1 คุณต้องเลื่อนลูกน้ำไปทางซ้ายสามหลัก:

2,1: 1000 = 0,0021

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001

การหารเศษส่วนทศนิยมด้วย 0.1, 0.01 และ 0.001 ก็ทำในลักษณะเดียวกับ ในการจ่ายเงินปันผลและตัวหาร คุณต้องย้ายจุดทศนิยมไปทางขวาตามหลักจำนวนเท่าที่อยู่หลังจุดทศนิยมในตัวหาร

ตัวอย่างเช่น ลองหาร 6.3 ด้วย 0.1 ก่อนอื่น ให้ย้ายเครื่องหมายจุลภาคในเงินปันผลและตัวหารไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ซึ่งหมายความว่าเราย้ายลูกน้ำในเงินปันผลและตัวหารไปทางขวาหนึ่งหลัก

หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เศษส่วนทศนิยม 6.3 จะกลายเป็นเลขปกติ 63 และเศษส่วนทศนิยม 0.1 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักจะกลายเป็นหนึ่ง และการหาร 63 ด้วย 1 นั้นง่ายมาก:

ซึ่งหมายความว่าค่าของนิพจน์ 6.3: 0.1 คือ 63

แต่มีวิธีที่สอง มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกย้ายไปทางขวาตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 6.3: 0.1. ลองดูตัวหารกัน. เราสนใจว่ามันมีศูนย์กี่ตัว เราเห็นว่ามีศูนย์หนึ่งตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 คุณต้องเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เลื่อนลูกน้ำไปทางขวาหนึ่งหลักแล้วได้ 63

ลองหาร 6.3 ด้วย 0.01 กัน ตัวหารของ 0.01 มีศูนย์สองตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 เราต้องเลื่อนจุดทศนิยมไปทางขวาสองหลัก แต่ในการจ่ายเงินปันผลจะมีเพียงหลักเดียวหลังจุดทศนิยม ในกรณีนี้ คุณต้องเพิ่มศูนย์อีกตัวที่ส่วนท้าย ผลลัพธ์ที่ได้คือ 630

ลองหาร 6.3 ด้วย 0.001 กัน ตัวหารของ 0.001 มีศูนย์สามตัว ซึ่งหมายความว่าในการจ่ายเงินปันผล 6.3 เราจำเป็นต้องเลื่อนจุดทศนิยมไปทางขวาสามหลัก:

6,3: 0,001 = 6300

งานสำหรับโซลูชันอิสระ

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกลุ่ม VKontakte ใหม่ของเราและเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่

เช่น:

± ดี ม … ง 1 ง 0 , ง -1 ง -2 …

โดยที่ ± คือเครื่องหมายเศษส่วน: + หรือ -

เป็นจุดทศนิยมที่ทำหน้าที่เป็นตัวคั่นระหว่างจำนวนเต็มและเศษส่วนของตัวเลข

ดีเค- ตัวเลขทศนิยม

ในกรณีนี้ ลำดับของตัวเลขก่อนจุดทศนิยม (ทางด้านซ้าย) จะมีจุดสิ้นสุด (เป็นค่าต่ำสุด 1 ต่อหลัก) และหลังจุดทศนิยม (ทางขวา) อาจเป็นค่าจำกัดทั้งคู่ (เป็นตัวเลือก อาจไม่มีตัวเลขหลังจุดทศนิยมเลย) และไม่มีที่สิ้นสุด

ค่าทศนิยม ± ดี ม … ง 1 ง 0 , ง -1 ง -2 … เป็นจำนวนจริง:

ซึ่งเท่ากับผลรวมของจำนวนพจน์ที่มีจำกัดหรือไม่จำกัด

การแสดงจำนวนจริงโดยใช้เศษส่วนทศนิยมเป็นลักษณะทั่วไปของการเขียนจำนวนเต็มในระบบเลขฐานสิบ การแสดงเลขฐานสิบของจำนวนเต็มไม่มีตัวเลขหลังจุดทศนิยม ดังนั้นการแสดงจึงมีลักษณะดังนี้:

± ดี ม … ง 1 ง 0 ,

และนี่เกิดขึ้นพร้อมกับการเขียนตัวเลขของเราในระบบเลขฐานสิบ

ทศนิยม- นี่คือผลลัพธ์ของการหาร 1 เป็น 10, 100, 1,000 และอื่นๆ เศษส่วนเหล่านี้ค่อนข้างสะดวกในการคำนวณเพราะว่า จะขึ้นอยู่กับระบบตำแหน่งเดียวกันกับการนับและการบันทึกจำนวนเต็ม ด้วยเหตุนี้สัญกรณ์และกฎสำหรับการทำงานกับเศษส่วนทศนิยมจึงเกือบจะเหมือนกับจำนวนเต็ม

เมื่อเขียนเศษส่วนทศนิยม คุณไม่จำเป็นต้องทำเครื่องหมายตัวส่วน แต่จะถูกกำหนดโดยตำแหน่งที่ถูกครอบครองโดยตัวเลขที่เกี่ยวข้อง ขั้นแรกเราเขียนส่วนหนึ่งของตัวเลขทั้งหมด จากนั้นจึงใส่จุดทศนิยมทางด้านขวา ตัวเลขตัวแรกหลังจุดทศนิยมระบุจำนวนหนึ่งในสิบ ตัวเลขที่สองคือจำนวนหนึ่งในร้อย ตัวเลขที่สามคือจำนวนหนึ่งในพัน และอื่นๆ ตัวเลขที่อยู่หลังจุดทศนิยมคือ ทศนิยม.

ตัวอย่างเช่น:

ข้อดีอย่างหนึ่งของเศษส่วนทศนิยมคือสามารถลดเป็นเศษส่วนธรรมดาได้อย่างง่ายดายมาก ตัวเลขหลังจุดทศนิยม (สำหรับเราคือ 5047) คือ เศษ; ตัวส่วนเท่ากับ n- ยกกำลัง 10 โดยที่ n- จำนวนตำแหน่งทศนิยม (สำหรับเราคือ n=4):

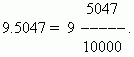
เมื่อไม่มีส่วนจำนวนเต็มในเศษส่วนทศนิยม เราจะใส่ศูนย์ไว้หน้าจุดทศนิยม:

คุณสมบัติของเศษส่วนทศนิยม

1. ทศนิยมจะไม่เปลี่ยนแปลงเมื่อมีการเพิ่มศูนย์ทางด้านขวา:

13.6 =13.6000.

2. ทศนิยมจะไม่เปลี่ยนแปลงเมื่อลบเลขศูนย์ที่อยู่ท้ายทศนิยมออก:

0.00123000 = 0.00123.

ความสนใจ!คุณไม่สามารถลบเลขศูนย์ที่ไม่ได้อยู่ที่ส่วนท้ายของเศษส่วนทศนิยมได้!

3. เศษส่วนทศนิยมเพิ่มขึ้น 10, 100, 1,000 และต่อๆ ไปเมื่อเราย้ายจุดทศนิยมไปที่ 1, 2, 2 และต่อๆ ไปในตำแหน่งทางด้านขวา ตามลำดับ:

3.675 → 367.5 (เศษส่วนเพิ่มขึ้นร้อยเท่า)

4. เศษส่วนทศนิยมจะกลายเป็นสิบ หนึ่งแสน และน้อยลงเรื่อยๆ เมื่อเราย้ายจุดทศนิยมไปที่ 1, 2, 3 และอื่นๆ ไปทางซ้าย ตามลำดับ:

1536.78 → 1.53678 (เศษส่วนนั้นเล็กลงหนึ่งพันเท่า)

ประเภทของเศษส่วนทศนิยม

เศษส่วนทศนิยมแบ่งออกเป็น สุดท้าย, ไม่มีที่สิ้นสุดและ ทศนิยมเป็นระยะ.

เศษส่วนทศนิยมสุดท้ายคือนี่คือเศษส่วนที่มีตัวเลขจำกัดหลังจุดทศนิยม (หรือไม่มีเลย) เช่น ดูเหมือนว่า:

จำนวนจริงสามารถแสดงเป็นเศษส่วนทศนิยมจำกัดได้ก็ต่อเมื่อจำนวนนี้เป็นจำนวนตรรกยะและเมื่อเขียนเป็นเศษส่วนลดไม่ได้ พี/คิวตัวส่วน ถามไม่มีตัวประกอบเฉพาะนอกจาก 2 และ 5

ทศนิยมอนันต์.

ประกอบด้วยกลุ่มตัวเลขที่เรียกซ้ำกันอย่างไม่สิ้นสุด ระยะเวลา- มหัพภาคเขียนอยู่ในวงเล็บ ตัวอย่างเช่น 0.12345123451234512345… = 0.(12345).

เศษส่วนทศนิยมเป็นระยะ- นี่คือเศษส่วนทศนิยมอนันต์ซึ่งลำดับของตัวเลขหลังจุดทศนิยมเริ่มต้นจากตำแหน่งใดตำแหน่งหนึ่งเป็นกลุ่มของตัวเลขที่ซ้ำกันเป็นระยะ กล่าวอีกนัยหนึ่ง เศษส่วนเป็นระยะ- เศษส่วนทศนิยมที่มีลักษณะดังนี้:

เศษส่วนดังกล่าวมักจะเขียนสั้น ๆ ดังนี้:

กลุ่มตัวเลข ข 1 … ข ลซึ่งซ้ำก็คือ ระยะเวลาของเศษส่วน, จำนวนหลักในกลุ่มนี้คือ ระยะเวลา.

เมื่ออยู่ในเศษส่วนคาบ ระยะเวลาจะมาหลังจุดทศนิยมทันที หมายความว่าเศษส่วนนั้นเท่ากับ บริสุทธิ์เป็นระยะ- เมื่อมีตัวเลขอยู่ระหว่างจุดทศนิยมกับช่วงที่ 1 เศษส่วนก็จะเป็น ผสมเป็นระยะและกลุ่มของตัวเลขหลังจุดทศนิยมขึ้นไปถึงหลักที่ 1 ของช่วงคือ เศษส่วนเบื้องต้น.

ตัวอย่างเช่นเศษส่วน 1,(23) = 1.2323... เป็นคาบบริสุทธิ์ และเศษส่วน 0.1(23) = 0.12323... เป็นคาบผสม

คุณสมบัติหลักของเศษส่วนคาบเนื่องจากเศษส่วนเหล่านี้แตกต่างจากเศษส่วนทศนิยมทั้งชุด จึงอยู่ที่ข้อเท็จจริงที่ว่าเศษส่วนเป็นคาบและมีเพียงเศษส่วนเท่านั้นที่แสดงถึงจำนวนตรรกยะ แม่นยำยิ่งขึ้นสิ่งต่อไปนี้เกิดขึ้น:

เศษส่วนทศนิยมที่มีคาบเป็นอนันต์ใดๆ แสดงถึงจำนวนตรรกยะ ในทางกลับกัน เมื่อจำนวนตรรกยะถูกขยายเป็นเศษส่วนทศนิยมอนันต์ เศษส่วนนี้จะเป็นเศษส่วน

ในบทความนี้ เราจะมาทำความเข้าใจว่าเศษส่วนทศนิยมคืออะไร มีคุณลักษณะและคุณสมบัติอะไรบ้าง ไป!

เศษส่วนทศนิยมเป็นกรณีพิเศษของเศษส่วนสามัญ (โดยที่ตัวส่วนเป็นผลคูณของ 10)

คำนิยาม

ทศนิยมคือเศษส่วนที่มีตัวส่วนเป็นตัวเลขที่ประกอบด้วยหนึ่งและจำนวนศูนย์ตามหลัง นั่นคือเศษส่วนเหล่านี้เป็นเศษส่วนที่มีตัวส่วนเป็น 10, 100, 1,000 เป็นต้น มิฉะนั้น เศษส่วนทศนิยมสามารถกำหนดลักษณะเป็นเศษส่วนที่มีตัวส่วนเป็น 10 หรือหนึ่งในกำลังของสิบ

ตัวอย่างเศษส่วน:

, ,

เศษส่วนทศนิยมเขียนแตกต่างจากเศษส่วนธรรมดา การดำเนินการกับเศษส่วนเหล่านี้ก็แตกต่างจากการดำเนินการกับเศษส่วนทั่วไปเช่นกัน กฎสำหรับการดำเนินการกับกฎเหล่านั้นส่วนใหญ่จะคล้ายกับกฎสำหรับการดำเนินการกับจำนวนเต็ม โดยเฉพาะอย่างยิ่งสิ่งนี้อธิบายถึงความต้องการในการแก้ปัญหาเชิงปฏิบัติ

การแสดงเศษส่วนในรูปแบบทศนิยม

เศษส่วนทศนิยมไม่มีตัวส่วน แต่จะแสดงจำนวนตัวเศษ โดยทั่วไปเศษส่วนทศนิยมจะถูกเขียนตามรูปแบบต่อไปนี้:

โดยที่ X เป็นส่วนจำนวนเต็มของเศษส่วน Y เป็นส่วนที่เป็นเศษส่วน “” คือจุดทศนิยม

หากต้องการแสดงเศษส่วนเป็นทศนิยมอย่างถูกต้อง จะต้องเป็นเศษส่วนปกติ กล่าวคือ โดยเน้นส่วนจำนวนเต็ม (ถ้าเป็นไปได้) และตัวเศษที่น้อยกว่าตัวส่วน จากนั้นในรูปแบบทศนิยม ส่วนจำนวนเต็มจะถูกเขียนก่อนจุดทศนิยม (X) และตัวเศษของเศษส่วนร่วมจะเขียนหลังจุดทศนิยม (Y)

หากตัวเศษมีตัวเลขที่มีหลักน้อยกว่าจำนวนศูนย์ในตัวส่วน ดังนั้นในส่วน Y จำนวนหลักที่ขาดหายไปในรูปแบบทศนิยมจะถูกเติมด้วยศูนย์ที่อยู่ข้างหน้าตัวเลขตัวเศษ

ตัวอย่าง:

หากเศษส่วนสามัญน้อยกว่า 1 นั่นคือ ไม่มีส่วนจำนวนเต็ม ดังนั้นสำหรับ X ในรูปแบบทศนิยมให้เขียน 0

ในส่วนเศษส่วน (Y) หลังจากเลขนัยสำคัญสุดท้าย (ไม่ใช่ศูนย์) คุณสามารถป้อนเลขศูนย์ได้ตามใจชอบ ซึ่งไม่ส่งผลต่อค่าของเศษส่วน ในทางกลับกัน คุณสามารถละเว้นศูนย์ทั้งหมดที่ส่วนท้ายของเศษส่วนของทศนิยมได้

การอ่านทศนิยม

โดยทั่วไปส่วนที่ X จะอ่านได้ดังนี้: “X integers”

ส่วน Y อ่านตามตัวเลขในตัวส่วน สำหรับตัวส่วน 10 คุณควรอ่าน: “Y ในสิบ” สำหรับตัวส่วน 100: “Y ในร้อย” สำหรับตัวส่วน 1,000: “Y ในพัน” และอื่นๆ... 😉

อีกวิธีหนึ่งในการอ่านโดยพิจารณาจากจำนวนหลักของเศษส่วนนั้นถือว่าถูกต้องมากกว่า ในการทำเช่นนี้ คุณต้องเข้าใจว่าตัวเลขเศษส่วนนั้นอยู่ในภาพสะท้อนในกระจก เทียบกับตัวเลขของเศษส่วนทั้งหมด

ชื่อของการอ่านที่ถูกต้องมีอยู่ในตาราง:

จากนี้การอ่านควรเป็นไปตามชื่อหลักของหลักสุดท้ายของส่วนเศษส่วน

• 3.5 อ่านว่า "สามจุดห้า"
• 0.016 อ่านว่า "ศูนย์จุดหนึ่งหมื่นหกพัน"

การแปลงเศษส่วนตามอำเภอใจให้เป็นทศนิยม

ถ้าตัวส่วนของเศษส่วนร่วมคือ 10 หรือยกกำลังสิบ เศษส่วนนั้นจะถูกแปลงตามที่อธิบายไว้ข้างต้น ในสถานการณ์อื่นๆ จำเป็นต้องมีการเปลี่ยนแปลงเพิ่มเติม

การแปลมี 2 วิธี

วิธีการถ่ายโอนครั้งแรก

ตัวเศษและส่วนจะต้องคูณด้วยจำนวนเต็มจนตัวส่วนสร้างเลข 10 หรือหนึ่งในกำลังของสิบ จากนั้นเศษส่วนจะแสดงในรูปแบบทศนิยม

วิธีนี้สามารถใช้ได้กับเศษส่วนที่ตัวส่วนสามารถขยายเป็น 2 และ 5 ได้เท่านั้น ดังนั้น ในตัวอย่างก่อนหน้านี้ - หากการขยายตัวมีปัจจัยสำคัญอื่น ๆ (เช่น ) คุณจะต้องหันไปใช้วิธีที่ 2

วิธีการแปลที่สอง

วิธีที่ 2 คือการหารตัวเศษด้วยตัวส่วนในคอลัมน์หรือบนเครื่องคิดเลข ส่วนทั้งหมด (ถ้ามี) จะไม่มีส่วนร่วมในการเปลี่ยนแปลง

กฎสำหรับการหารยาวที่ทำให้เกิดเศษส่วนทศนิยมมีอธิบายไว้ด้านล่าง (ดูการหารทศนิยม)

การแปลงเศษส่วนทศนิยมให้เป็นเศษส่วนร่วม

ในการทำเช่นนี้ คุณควรเขียนเศษส่วนของมัน (ทางด้านขวาของจุดทศนิยม) เป็นตัวเศษ และผลลัพธ์ของการอ่านเศษส่วนเป็นตัวเลขที่สอดคล้องกันในตัวส่วน ต่อไป หากเป็นไปได้ คุณจะต้องลดเศษส่วนผลลัพธ์ลง

เศษส่วนทศนิยมที่มีขอบเขตจำกัดและอนันต์

เศษส่วนทศนิยมเรียกว่าเศษส่วนสุดท้าย ซึ่งเป็นส่วนที่ประกอบด้วยตัวเลขจำนวนจำกัด

ตัวอย่างทั้งหมดข้างต้นมีเศษส่วนทศนิยมสุดท้าย อย่างไรก็ตาม ไม่ใช่ทุกเศษส่วนธรรมดาที่สามารถแสดงเป็นทศนิยมสุดท้ายได้ หากวิธีการแปลงที่ 1 ไม่สามารถใช้ได้กับเศษส่วนที่กำหนด และวิธีที่ 2 แสดงให้เห็นว่าไม่สามารถหารได้สำเร็จ ก็จะได้เฉพาะเศษส่วนทศนิยมอนันต์เท่านั้น

เป็นไปไม่ได้ที่จะเขียนเศษส่วนอนันต์ให้อยู่ในรูปที่สมบูรณ์ ในรูปแบบที่ไม่สมบูรณ์สามารถแสดงเศษส่วนดังกล่าวได้:

1. อันเป็นผลมาจากการลดจำนวนทศนิยมตามที่ต้องการ
2. เป็นเศษส่วนคาบ

เศษส่วนเรียกว่าคาบหากหลังจากจุดทศนิยมแล้วก็สามารถแยกแยะลำดับของตัวเลขที่ซ้ำกันไม่รู้จบได้

เศษส่วนที่เหลือเรียกว่าไม่เป็นคาบ สำหรับเศษส่วนที่ไม่ใช่คาบ อนุญาตให้ใช้เฉพาะวิธีการแสดงแบบที่ 1 (การปัดเศษ) เท่านั้น

ตัวอย่างของเศษส่วนเป็นคาบ: 0.8888888... นี่คือเลขซ้ำ 8 ซึ่งเห็นได้ชัดว่าจะถูกทำซ้ำอย่างไม่สิ้นสุดเนื่องจากไม่มีเหตุผลที่จะถือว่าเป็นอย่างอื่น ตัวเลขนี้เรียกว่า ระยะเวลาของเศษส่วน.

เศษส่วนเป็นคาบอาจเป็นแบบบริสุทธิ์หรือแบบผสมก็ได้ เศษส่วนทศนิยมบริสุทธิ์คือเศษส่วนที่ระยะเวลาเริ่มต้นทันทีหลังจากจุดทศนิยม เศษส่วนคละมีตัวเลข 1 หลักขึ้นไปก่อนจุดทศนิยม

54.33333… – เศษส่วนทศนิยมบริสุทธิ์เป็นงวด

2.5621212121… – เศษส่วนคละคาบ

ตัวอย่างการเขียนเศษส่วนทศนิยมอนันต์:

ตัวอย่างที่ 2 แสดงวิธีการจัดรูปแบบช่วงเวลาในการเขียนเศษส่วนแบบคาบให้ถูกต้อง

การแปลงเศษส่วนทศนิยมคาบเป็นเศษส่วนสามัญ

ในการแปลงเศษส่วนคาบบริสุทธิ์เป็นคาบปกติ ให้เขียนมันลงในตัวเศษ และเขียนตัวเลขที่ประกอบด้วยเก้าเป็นจำนวนเท่ากับจำนวนหลักในช่วงเวลานั้นเป็นตัวส่วน

เศษส่วนทศนิยมคาบแบบผสมมีการแปลดังนี้:

1. คุณต้องสร้างตัวเลขที่ประกอบด้วยตัวเลขหลังจุดทศนิยมก่อนจุดและจุดแรก
2. จากตัวเลขผลลัพธ์ ให้ลบตัวเลขหลังจุดทศนิยมก่อนจุด ผลลัพธ์จะเป็นตัวเศษของเศษส่วนร่วม
3. ในตัวหารคุณต้องป้อนตัวเลขที่ประกอบด้วยตัวเลขเก้าเท่ากับจำนวนหลักของงวดตามด้วยศูนย์จำนวนซึ่งเท่ากับจำนวนหลักของตัวเลขหลังจุดทศนิยมก่อนวันที่ 1 ระยะเวลา.

การเปรียบเทียบทศนิยม

เศษส่วนทศนิยมจะถูกเปรียบเทียบเริ่มแรกด้วยส่วนทั้งหมด เศษส่วนที่มีส่วนทั้งหมดมากกว่าย่อมมากกว่า

หากส่วนจำนวนเต็มเท่ากัน ให้เปรียบเทียบหลักของหลักที่สอดคล้องกันของส่วนที่เป็นเศษส่วน โดยเริ่มจากส่วนแรก (จากส่วนสิบ) ใช้หลักการเดียวกันนี้: เศษส่วนที่มากกว่าคือเศษส่วนที่มีมากกว่าในสิบ; ถ้าหลักสิบเท่ากัน ก็เปรียบเทียบหลักร้อย และอื่นๆ

เพราะว่า

เนื่องจากเศษส่วนที่ 2 มีเศษส่วนเท่ากันและมีเศษในสิบเท่ากัน เศษส่วนที่ 2 จึงมีค่าในร้อยมากกว่า

การบวกและการลบทศนิยม

การบวกและการลบทศนิยมในลักษณะเดียวกับจำนวนเต็มโดยการเขียนตัวเลขที่สอดคล้องกันไว้ข้างใต้กัน ในการดำเนินการนี้ คุณจะต้องมีจุดทศนิยมอยู่ต่ำกว่ากัน จากนั้นหน่วย (สิบ ฯลฯ ) ของส่วนจำนวนเต็มและส่วนสิบ (ส่วนร้อย ฯลฯ ) ของเศษส่วนจะเป็นไปตามนั้น ตัวเลขที่หายไปของส่วนที่เป็นเศษส่วนจะเต็มไปด้วยศูนย์ โดยตรง กระบวนการบวกและการลบจะดำเนินการในลักษณะเดียวกับจำนวนเต็ม

การคูณทศนิยม

ในการคูณทศนิยม คุณต้องเขียนไว้ใต้อีกอัน โดยให้สอดคล้องกับหลักสุดท้ายและไม่สนใจตำแหน่งของจุดทศนิยม จากนั้นคุณต้องคูณตัวเลขในลักษณะเดียวกับการคูณจำนวนเต็ม หลังจากได้รับผลลัพธ์แล้วควรคำนวณจำนวนหลักหลังจุดทศนิยมใหม่ในเศษส่วนทั้งสองและแยกจำนวนเศษส่วนทั้งหมดในตัวเลขผลลัพธ์ด้วยลูกน้ำ หากมีตัวเลขไม่เพียงพอ จะถูกแทนที่ด้วยศูนย์

การคูณและหารทศนิยมด้วย 10n

การกระทำเหล่านี้ทำได้ง่ายและค่อยๆ ขยับจุดทศนิยม ป เมื่อคูณ จุดทศนิยมจะเลื่อนไปทางขวา (เศษส่วนเพิ่มขึ้น) ด้วยตัวเลขหลักเท่ากับจำนวนศูนย์ใน 10n โดยที่ n คือจำนวนเต็มตามอำเภอใจ นั่นคือตัวเลขจำนวนหนึ่งจะถูกถ่ายโอนจากส่วนที่เป็นเศษส่วนไปยังส่วนทั้งหมด เมื่อทำการหารลูกน้ำจะถูกย้ายไปทางซ้าย (จำนวนลดลง) และตัวเลขบางส่วนจะถูกโอนจากส่วนจำนวนเต็มไปยังส่วนที่เป็นเศษส่วน หากมีตัวเลขไม่เพียงพอที่จะถ่ายโอน บิตที่หายไปจะถูกเติมด้วยศูนย์

การหารทศนิยมและจำนวนเต็มด้วยจำนวนเต็มและทศนิยม

การหารทศนิยมด้วยจำนวนเต็มจะคล้ายกับการหารจำนวนเต็มสองตัว นอกจากนี้ คุณจะต้องคำนึงถึงตำแหน่งของจุดทศนิยมเท่านั้น: เมื่อลบหลักของตำแหน่งที่ตามด้วยลูกน้ำ คุณต้องวางลูกน้ำไว้หลังตัวเลขปัจจุบันของคำตอบที่สร้างขึ้น ถัดไปคุณต้องหารต่อไปจนกว่าคุณจะได้ศูนย์ หากมีสัญญาณการจ่ายเงินปันผลไม่เพียงพอสำหรับการหารทั้งหมด ควรใช้ศูนย์แทน

ในทำนองเดียวกัน จำนวนเต็ม 2 ตัวจะถูกแบ่งออกเป็นคอลัมน์หนึ่ง หากตัวเลขหลักทั้งหมดของเงินปันผลถูกลบออกและการหารทั้งหมดยังไม่เสร็จสิ้น ในกรณีนี้ หลังจากลบตัวเลขหลักสุดท้ายของการจ่ายเงินปันผลแล้ว จุดทศนิยมจะถูกวางไว้ในคำตอบที่ได้ และใช้เลขศูนย์เป็นตัวเลขที่ลบออก เหล่านั้น. การจ่ายเงินปันผลตรงนี้จะแสดงเป็นเศษส่วนทศนิยมโดยมีเศษส่วนเป็นศูนย์

หากต้องการหารเศษส่วนทศนิยม (หรือจำนวนเต็ม) ด้วยเลขทศนิยม คุณต้องคูณเงินปันผลและตัวหารด้วยจำนวน 10 n ซึ่งจำนวนศูนย์จะเท่ากับจำนวนหลักหลังจุดทศนิยมในตัวหาร ด้วยวิธีนี้ คุณจะกำจัดจุดทศนิยมที่เป็นเศษส่วนที่คุณต้องการหารด้วย นอกจากนี้ กระบวนการแบ่งส่วนยังเกิดขึ้นพร้อมกับที่อธิบายไว้ข้างต้น

การแสดงทศนิยมแบบกราฟิก

เศษส่วนทศนิยมจะแสดงเป็นกราฟิกโดยใช้เส้นพิกัด เมื่อต้องการทำเช่นนี้ แต่ละส่วนจะถูกแบ่งออกเป็น 10 ส่วนเท่าๆ กัน เช่นเดียวกับการทำเครื่องหมายเซนติเมตรและมิลลิเมตรพร้อมกันบนไม้บรรทัด เพื่อให้แน่ใจว่ามีการแสดงทศนิยมอย่างถูกต้องและสามารถเปรียบเทียบได้อย่างเป็นกลาง

เพื่อให้การแบ่งส่วนในแต่ละส่วนเหมือนกัน คุณควรพิจารณาความยาวของส่วนเดียวอย่างรอบคอบ ควรเป็นเช่นนั้นเพื่อให้มั่นใจได้ถึงความสะดวกในการแบ่งเพิ่มเติม

เศษส่วนเขียนในรูปแบบ 0.8; 0.13; 2.856; 5.2; 0.04 เรียกว่าทศนิยม ที่จริงแล้ว ทศนิยมเป็นสัญลักษณ์แบบง่ายสำหรับเศษส่วนสามัญ สัญกรณ์นี้สะดวกที่จะใช้กับเศษส่วนทุกตัวที่มีตัวส่วนเป็น 10, 100, 1,000 และอื่นๆ

ลองดูตัวอย่าง (0.5 อ่านว่าศูนย์จุดห้า)

(0.15 อ่านเป็น ศูนย์จุดสิบห้า)

(5.3 อ่านว่า ห้าจุดสาม)

โปรดทราบว่าในรูปแบบเศษส่วนทศนิยม เครื่องหมายจุลภาคจะแยกส่วนจำนวนเต็มของตัวเลขออกจากส่วนที่เป็นเศษส่วน ส่วนจำนวนเต็มของเศษส่วนแท้คือ 0 สัญลักษณ์ของส่วนเศษส่วนของเศษส่วนทศนิยมจะมีตัวเลขได้มากเท่ากับ มีศูนย์อยู่ในสัญกรณ์ตัวส่วนของเศษส่วนสามัญที่สอดคล้องกัน

ลองดูตัวอย่าง , , .

ในบางกรณี อาจจำเป็นต้องถือว่าจำนวนธรรมชาติเป็นทศนิยมซึ่งมีเศษส่วนเป็นศูนย์ เป็นเรื่องปกติที่จะเขียนว่า 5 = 5.0; 245 = 245.0 และอื่นๆ โปรดทราบว่าในรูปแบบทศนิยมของจำนวนธรรมชาติ หน่วยของหลักที่มีนัยสำคัญน้อยที่สุดจะน้อยกว่าหน่วยของหลักที่มีนัยสำคัญที่สุดที่อยู่ติดกัน 10 เท่า คุณสมบัติเดียวกันนี้ใช้กับการเขียนเศษส่วนทศนิยม ดังนั้น ทันทีหลังจุดทศนิยมจะมีตำแหน่งหนึ่งในสิบ จากนั้นตำแหน่งหนึ่งในร้อย จากนั้นตำแหน่งหนึ่งในพัน และอื่นๆ ด้านล่างนี้เป็นชื่อของตัวเลข 31.85431 สองคอลัมน์แรกเป็นส่วนจำนวนเต็ม คอลัมน์ที่เหลือเป็นส่วนเศษส่วน

เศษส่วนนี้อ่านว่าสามสิบเอ็ดจุดแปดหมื่นห้าพันสี่ร้อยสามสิบเอ็ดแสน

การบวกและการลบทศนิยม

วิธีแรกคือการแปลงเศษส่วนทศนิยมเป็นเศษส่วนสามัญแล้วทำการบวก

ดังที่เห็นได้จากตัวอย่าง วิธีนี้ไม่สะดวกมากและควรใช้วิธีที่สองซึ่งถูกต้องมากกว่าโดยไม่ต้องแปลงเศษส่วนทศนิยมให้เป็นเศษส่วนธรรมดา หากต้องการบวกเศษส่วนทศนิยม 2 ตัว คุณต้อง:

• ทำให้จำนวนหลักหลังจุดทศนิยมเท่ากันในเงื่อนไข
• เขียนพจน์หนึ่งไว้ข้างใต้เพื่อให้แต่ละหลักของเทอมที่สองอยู่ใต้ตัวเลขที่สอดคล้องกันของเทอมแรก
• เพิ่มตัวเลขผลลัพธ์แบบเดียวกับที่คุณบวกจำนวนธรรมชาติ
• ใส่เครื่องหมายจุลภาคในผลรวมผลลัพธ์ใต้เครื่องหมายจุลภาคในเงื่อนไข

ลองดูตัวอย่าง:

• ทำให้จำนวนหลักหลังจุดทศนิยมเท่ากันใน minuend และ subtrahend
• เขียนส่วนย่อยใต้ minuend เพื่อให้แต่ละหลักของ subtrahend อยู่ใต้หลักที่สอดคล้องกันของ minuend
• ดำเนินการลบในลักษณะเดียวกับการลบจำนวนธรรมชาติ
• ใส่ลูกน้ำในผลต่างที่เกิดขึ้นใต้ลูกน้ำใน minuend และ subtrahend

ลองดูตัวอย่าง:

ในตัวอย่างที่กล่าวถึงข้างต้น จะเห็นได้ว่าการบวกและการลบเศษส่วนทศนิยมดำเนินการทีละนิด นั่นคือในลักษณะเดียวกับที่เราทำการดำเนินการที่คล้ายกันกับจำนวนธรรมชาติ นี่คือข้อได้เปรียบหลักของการเขียนเศษส่วนในรูปแบบทศนิยม

การคูณทศนิยม

ในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 และอื่นๆ คุณต้องย้ายจุดทศนิยมในเศษส่วนนี้ไปทางขวาด้วย 1, 2, 3 และอื่นๆ ตามลำดับ ดังนั้น หากลูกน้ำถูกย้ายไปทางขวา 1, 2, 3 และต่อๆ ไปในหลัก เศษส่วนก็จะเพิ่มขึ้นตามลำดับ 10, 100, 1,000 และต่อๆ ไป ในการคูณเศษส่วนทศนิยมสองส่วน คุณต้อง:

• คูณมันเป็นจำนวนธรรมชาติโดยไม่สนใจลูกน้ำ
• ในผลลัพธ์ที่ได้ ให้คั่นตัวเลขทางด้านขวาด้วยเครื่องหมายจุลภาคเท่าที่มีหลังเครื่องหมายจุลภาคในทั้งสองตัวรวมกัน

มีหลายกรณีที่ผลิตภัณฑ์มีตัวเลขน้อยกว่าที่ต้องคั่นด้วยเครื่องหมายจุลภาค จำนวนศูนย์ที่ต้องการจะถูกเพิ่มทางด้านซ้ายก่อนผลิตภัณฑ์นี้ จากนั้นลูกน้ำจะถูกย้ายไปทางซ้ายตามจำนวนหลักที่ต้องการ

ลองดูตัวอย่าง: 2 * 4 = 8 จากนั้น 0.2 * 0.4 = 0.08; 23 * 35 = 805 จากนั้น 0.023 * 0.35 = 0.00805

มีหลายกรณีที่ตัวคูณตัวใดตัวหนึ่งมีค่าเท่ากับ 0.1; 0.01; 0.001 เป็นต้น จะสะดวกกว่าถ้าใช้กฎต่อไปนี้

• หากต้องการคูณทศนิยมด้วย 0.1; 0.01; 0.001 เป็นต้นไป ในเศษส่วนทศนิยมนี้ คุณต้องเลื่อนจุดทศนิยมไปทางซ้าย 1, 2, 3 ไปเรื่อยๆ ตามลำดับ

ลองดูตัวอย่าง: 2.65 * 0.1 = 0.265; 457.6 * 0.01 = 4.576

คุณสมบัติของการคูณของจำนวนธรรมชาติยังใช้กับเศษส่วนทศนิยมด้วย

• เอบี = บา- สมบัติการสับเปลี่ยนของการคูณ
• (ab) ค = ก (bc)- สมบัติการเชื่อมโยงของการคูณ
• ก (b + c) = ab + acเป็นสมบัติการแจกแจงของการคูณเทียบกับการบวก

การหารทศนิยม

เป็นที่รู้กันว่าถ้าคุณหารจำนวนธรรมชาติ กเป็นจำนวนธรรมชาติ ขหมายถึงการหาจำนวนธรรมชาติดังกล่าว คซึ่งเมื่อคูณด้วย ขให้ตัวเลข ก- กฎข้อนี้ยังคงเป็นจริงหากมีตัวเลขอย่างน้อยหนึ่งตัว ก ข คเป็นเศษส่วนทศนิยม

ลองดูตัวอย่าง: คุณต้องหาร 43.52 ด้วย 17 ด้วยมุม โดยไม่สนใจลูกน้ำ ในกรณีนี้ ควรวางลูกน้ำในผลหารทันทีก่อนหลักแรกหลังจากใช้จุดทศนิยมในการจ่ายเงินปันผล

มีหลายกรณีที่เงินปันผลน้อยกว่าตัวหาร ส่วนจำนวนเต็มของผลหารจะเท่ากับศูนย์ ลองดูตัวอย่าง:

ลองดูอีกตัวอย่างที่น่าสนใจ

กระบวนการแบ่งได้หยุดลงเนื่องจากตัวเลขเงินปันผลหมดและส่วนที่เหลือไม่มีศูนย์ เป็นที่ทราบกันดีว่าเศษส่วนทศนิยมจะไม่เปลี่ยนแปลงหากมีการเพิ่มศูนย์จำนวนใด ๆ ทางด้านขวา ปรากฏชัดว่าจำนวนเงินปันผลไม่สิ้นสุด

ในการที่จะหารเศษส่วนทศนิยมด้วย 10, 100, 1,000 และอื่นๆ คุณจะต้องย้ายจุดทศนิยมในเศษส่วนนี้ไปทางซ้าย 1, 2, 3 และอื่นๆ ตามหลัก ลองดูตัวอย่าง: 5.14: 10 = 0.514; 2: 100 = 0.02; 37.51: 1,000 = 0.03751

หากเงินปันผลและตัวหารเพิ่มขึ้นพร้อมกัน 10, 100, 1,000 และต่อเนื่องไปเรื่อยๆ ผลหารจะไม่เปลี่ยนแปลง

ลองพิจารณาตัวอย่าง: 39.44: 1.6 = 24.65 เพิ่มเงินปันผลและตัวหาร 10 เท่า 394.4: 16 = 24.65 ควรสังเกตว่าการหารเศษส่วนทศนิยมด้วยจำนวนธรรมชาติในตัวอย่างที่สองนั้นง่ายกว่า

หากต้องการหารเศษส่วนทศนิยมคุณต้อง:

• ย้ายลูกน้ำในเงินปันผลและตัวหารไปทางขวาตามหลักจำนวนเท่าที่มีหลังจุดทศนิยมในตัวหาร
• หารด้วยจำนวนธรรมชาติ

ลองพิจารณาตัวอย่าง: 23.6: 0.02 โปรดทราบว่าตัวหารมีทศนิยมสองตำแหน่ง ดังนั้นเราจึงคูณตัวเลขทั้งสองด้วย 100 และได้ 2360: 2 = 1180 หารผลลัพธ์ด้วย 100 แล้วได้คำตอบ 11.80 หรือ 23.6: 0, 02 = 11.8.

การเปรียบเทียบทศนิยม

มีสองวิธีในการเปรียบเทียบทศนิยม วิธีแรก คุณต้องเปรียบเทียบเศษส่วนทศนิยมสองตัว 4.321 และ 4.32 ทำให้จำนวนตำแหน่งทศนิยมเท่ากัน และเริ่มเปรียบเทียบทีละตำแหน่ง สิบกับสิบ ร้อยกับร้อย และอื่นๆ ในที่สุดเราก็ได้ 4.321 > 4.320

วิธีที่สองในการเปรียบเทียบเศษส่วนทศนิยมทำได้โดยใช้การคูณ คูณตัวอย่างข้างต้นด้วย 1,000 และเปรียบเทียบ 4321 > 4320 วิธีใดสะดวกกว่าทุกคนเลือกเอง

กลับ